Question

If $f(\theta) = |\sin\theta + 1| + |\sin\theta - 2| + |\sin\theta - 1| + |\sin\theta - 3|$ where $0 \leq \theta \leq 2\pi$, then the sum of maximum and minimum value of $f(\theta)$ is

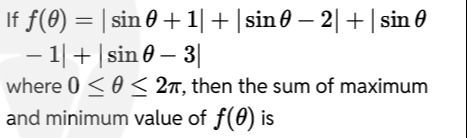
Answer 1

14

Answer 2

Let $x = \sin\theta$. The range of $x$ is $[-1, 1]$. The function simplifies to $f(x) = 7-2x$ for $x \in [-1, 1]$. This is a decreasing linear function. Its maximum value on $[-1, 1]$ is $f(-1)=9$ and its minimum value is $f(1)=5$. The sum of these values is $9+5=14$.