Solveeit Logo
Login

Question

Question: If from any point \(P,\) tangents \(PT,P{T}'\) are drawn to two given circles with centers \(A\) and...

If from any point P,P, tangents PT,PT′PT,P{T}' are drawn to two given circles with centers AA and BB respectively; and if PNPN is the perpendicular from PP on their radical axis, then PT2−PT′2=P{{T}^{2}}-P{{{T}'}^{2}}=
(a)2.PN.AB\left( a \right) 2.PN.AB
(b)4.PN.AB\left( b \right) 4.PN.AB
(c)PN.AB\left( c \right) PN.AB
(d)\left( d \right) None of these

Explanation

Solution

We will write the equations of the given two circles. Then we will find the line joining the centers of the two circles. Then, we will find the equation of the tangents. Then, we will find the equation of the radical axis. With this information, we can find the difference of the squares of the tangents.

Complete step-by-step answer:
Let us draw the diagram as follows:

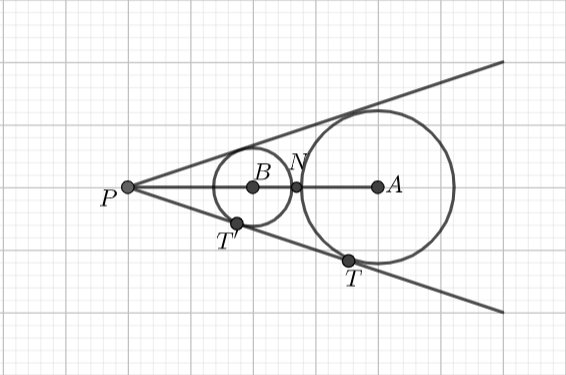
We need to write the equations of the two circles.
Let the equation of the first circle be x2+y2+2g1x+c=0.......(1){{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+c=0.......\left( 1 \right)
And let the equation of the second circle be x2+y2+2g2x+c=0.......(2){{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+c=0.......\left( 2 \right)
Then, we can say that the centers of the first and second circles are given by A(−g1,0)A\left( -{{g}_{1}},0 \right) and B(−g2,0)B\left( -{{g}_{2}},0 \right) respectively.
So, we will get AB=g1−g2.AB={{g}_{1}}-{{g}_{2}}.
Now, let us suppose that the point PP is given by the coordinates (x1,y1).\left( {{x}_{1}},{{y}_{1}} \right).
Then, we know that the tangent PTPT is given by PT=x12+y12+2g1x1+c.PT=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c}.
Similarly, we can write the tangent PT′P{T}' as PT′=x12+y12+2g2x1+c.P{T}'=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{2}}{{x}_{1}}+c}.
Now, we can find the radical axis of the given two circles by finding the difference of the equation (1)\left( 1 \right) and equation (2).\left( 2 \right).
Therefore, the radical axis of the circles is given by 2(g1−g2)x=02\left( {{g}_{1}}-{{g}_{2}} \right)x=0 or x=0.x=0.
We know that PNPN is the length of the perpendicular from PP on the radical axis x1.{{x}_{1}}.
Now, we will get PT2−PT′2=x12+y12+2g1x1+c−(x12+y12+2g2x1+c).P{{T}^{2}}-P{{{T}'}^{2}}={{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c-\left( {{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{2}}{{x}_{1}}+c \right).
We can write it as PT2−PT′2=x12+y12+2g1x1+c−x12−y12−2g2x1−c.P{{T}^{2}}-P{{{T}'}^{2}}={{x}_{1}}^{2}+{{y}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+c-{{x}_{1}}^{2}-{{y}_{1}}^{2}-2{{g}_{2}}{{x}_{1}}-c.
After cancelling the similar terms with opposite signs, we will get PT2−PT′2=2g1x1−2g2x1.P{{T}^{2}}-P{{{T}'}^{2}}=2{{g}_{1}}{{x}_{1}}-2{{g}_{2}}{{x}_{1}}.
From this, we will get PT2−PT′2=2x1(g1−g2).P{{T}^{2}}-P{{{T}'}^{2}}=2{{x}_{1}}\left( {{g}_{1}}-{{g}_{2}} \right).
So, we get PT2−PT′2=2.PN.AB.P{{T}^{2}}-P{{{T}'}^{2}}=2.PN.AB. $$$$
Hence the answer is 2.PN.AB.2.PN.AB.

Note: We know that the standard equation of a circle of radius rr and centered at a point (h,k)\left( h,k \right) is given by (x−h)2+(y−k)2=r2.{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}. The general equation of any type of circle is given by x2+y2+2gx+2fy+c=0,{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0, for all values of g,fg,f and c.c. If we add g2+f2{{g}^{2}}+{{f}^{2}} on both sides of the general equation and transposing cc from the LHS to the RHS will give the standard equation of a circle centered at (g,f)\left( g,f \right) with a radius of aa where g2+f2−c=a2.{{g}^{2}}+{{f}^{2}}-c={{a}^{2}}.