Question

If from any point on the common chord of two intersecting circles, tangents are drawn to the circles, prove that they are equal.

Answer 1

Firstly, we have to draw a figure according to the given data. In the figure, AB will be the common chord, P will be the point, PQ and PR will be the tangents. We have to show that these tangents are equal . For this, we will apply Intersecting Secant-Tangent Theorem which states that if a tangent segment and a secant segment are drawn to a circle from an exterior point, then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment. Using this theorem, we will get two equations whose RHS will be similar. By equating the LHSs, we will get the required proof.

Complete step by step answer:
We are given that tangents are drawn to two intersecting circles from a point that is drawn from their common chord. Let us illustrate this.

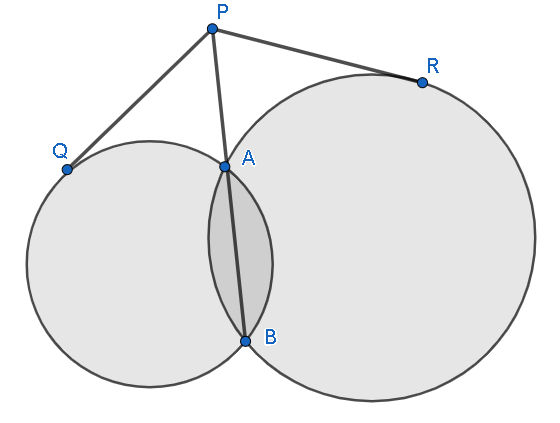
In the above figure, AB is the common chord, P is the point, PQ and PR are the tangents. We have to show $PQ=PR$ .
Let us apply the Intersecting Secant-Tangent Theorem. Intersecting Secant-Tangent Theorem states that if a tangent segment and a secant segment are drawn to a circle from an exterior point, then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment. From the above figure, let us consider tangent PQ and the secant PAB. Therefore, according to the Intersecting Secant-Tangent Theorem, we can write
$\Rightarrow P{{Q}^{2}}=PA\times PB...\left( i \right)$
Similarly, for the tangent PR and secant PAB, we can write
$\Rightarrow P{{R}^{2}}=PA\times PB...\left( ii \right)$
From equations (i) and (ii), we can equate the LHS since the RHS are similar.
$\Rightarrow P{{Q}^{2}}=P{{R}^{2}}$
Let us take the square root on both sides.
$\Rightarrow PQ=PR$
Thus, tangents drawn from any point on the common chord of two intersecting circles are equal.
Hence proved.

Note: Students must be through with the properties of circles and tangents. In questions similar to this type, they must draw figures according to the given information. Students have a chance of making a mistake by writing the Intersecting Secant-Tangent Theorem in equations (i) (or (ii) ) as $P{{Q}^{2}}=PA\times AB$ .