Solveeit Logo
Login

Question

Question: If $$ \frac{(x - 1)(x + 1)(x - 2)^2(e^{3x} - 1)}{x(3 - x)^3(x - 1)^2(x + 3)} \le 0 $$ the complete s...

If (x−1)(x+1)(x−2)2(e3x−1)x(3−x)3(x−1)2(x+3)≤0\frac{(x - 1)(x + 1)(x - 2)^2(e^{3x} - 1)}{x(3 - x)^3(x - 1)^2(x + 3)} \le 0 the complete solution set of values of x is

A

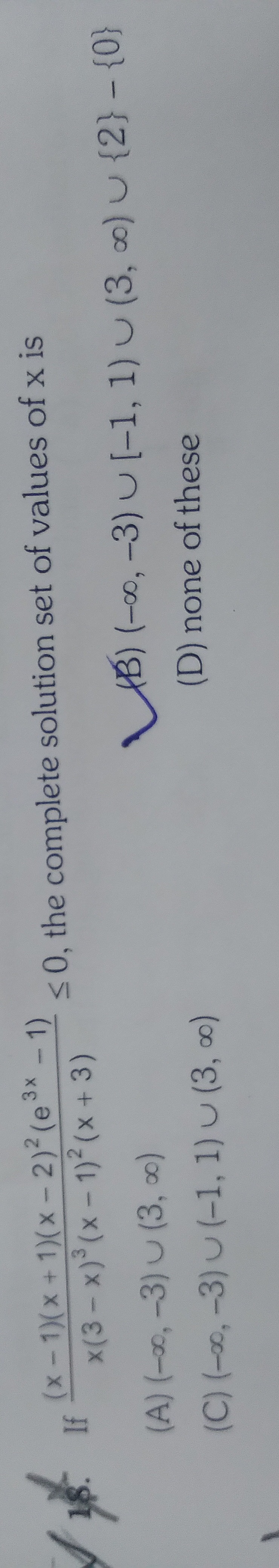
(−∞,−3)∪(3,∞)(-\infty, -3) \cup (3, \infty)

B

(−∞,−3)∪[−1,1]∪(3,∞)−{2}−{0}(-\infty, -3) \cup [-1, 1] \cup (3, \infty) - \{2\} - \{0\}

C

(−∞,−3)∪(−1,1)∪(3,∞)(-\infty, -3) \cup (-1, 1) \cup (3, \infty)

D

none of these

Answer

none of these

Explanation

Solution

The inequality is (x−1)(x+1)(x−2)2(e3x−1)x(3−x)3(x−1)2(x+3)≤0\frac{(x - 1)(x + 1)(x - 2)^2(e^{3x} - 1)}{x(3 - x)^3(x - 1)^2(x + 3)} \le 0 Critical points are x=−3,−1,0,1,2,3x = -3, -1, 0, 1, 2, 3. The expression simplifies to (x+1)(x−2)2(e3x−1)x(3−x)3(x−1)(x+3)≤0\frac{(x + 1)(x - 2)^2(e^{3x} - 1)}{x(3 - x)^3(x - 1)(x + 3)} \le 0 for x≠1x \ne 1. Sign analysis in intervals: (−∞,−3)(-\infty, -3): + (−3,−1)(-3, -1): - (−1,0)(-1, 0): + (0,1)(0, 1): - (1,2)(1, 2): + (2,3)(2, 3): + (3,∞)(3, \infty): - The expression is negative in (−3,−1)(-3, -1), (0,1)(0, 1), and (3,∞)(3, \infty). The expression is zero when the numerator is zero and the denominator is non-zero. Numerator zero at x=−1x = -1 (denominator non-zero) and x=2x = 2 (denominator non-zero). Thus, x=−1x = -1 and x=2x = 2 are included. The expression is undefined at x=−3,0,1,3x = -3, 0, 1, 3. The solution set is (−3,−1]∪(0,1)∪{2}∪(3,∞)(-3, -1] \cup (0, 1) \cup \{2\} \cup (3, \infty). This set is not among the options.