Solveeit Logo
Login

Question

Question: If $\frac{log x}{b-c}=\frac{log y}{c-a}=\frac{log z}{a-b}$, then which of the following is true...

If logxb−c=logyc−a=logza−b\frac{log x}{b-c}=\frac{log y}{c-a}=\frac{log z}{a-b}, then which of the following is true

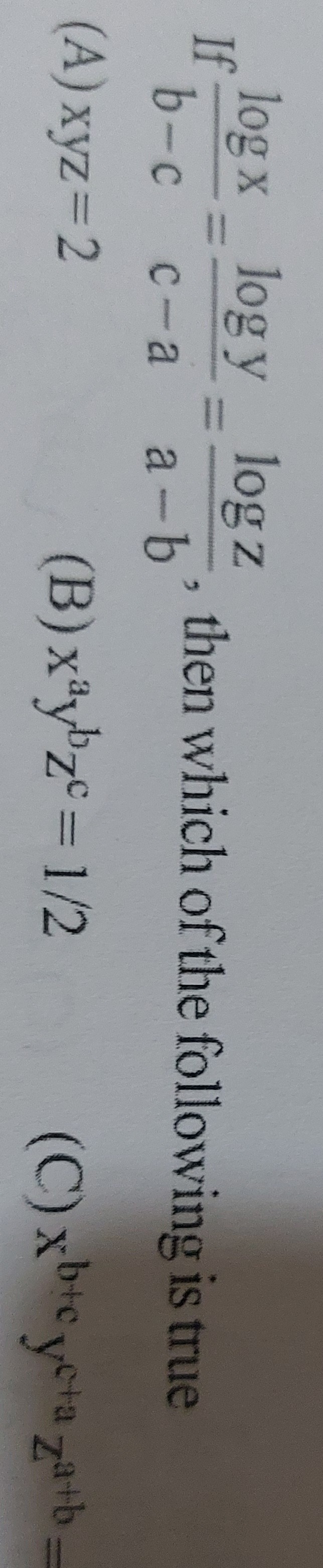
A

xyz=2

B

xaybzcx^{a}y^{b}z^{c} = 1/2

C

xb+cyc+aza+bx^{b+c}y^{c+a}z^{a+b} = 1

Answer

$x^{b+c}y^{c+a}z^{a+b}=1

Explanation

Solution

Given:

log⁡xb−c=log⁡yc−a=log⁡za−b=k.\frac{\log x}{b-c}=\frac{\log y}{c-a}=\frac{\log z}{a-b}=k.

Thus:

log⁡x=k(b−c),log⁡y=k(c−a),log⁡z=k(a−b).\log x = k(b-c), \quad \log y=k(c-a), \quad \log z=k(a-b).

Exponentiating:

x=ek(b−c),y=ek(c−a),z=ek(a−b).x=e^{k(b-c)}, \quad y=e^{k(c-a)}, \quad z=e^{k(a-b)}.

We need to evaluate:

xb+cyc+aza+b.x^{b+c}y^{c+a}z^{a+b}.

Taking natural logarithm,

ln⁡(xb+cyc+aza+b)=(b+c)ln⁡x+(c+a)ln⁡y+(a+b)ln⁡z.\ln\left(x^{b+c}y^{c+a}z^{a+b}\right) = (b+c)\ln x+(c+a)\ln y+(a+b)\ln z.

Substitute the values:

=(b+c)k(b−c)+(c+a)k(c−a)+(a+b)k(a−b).= (b+c)k(b-c) + (c+a)k(c-a) + (a+b)k(a-b).

Note that:

(b+c)(b−c)=b2−c2,(c+a)(c−a)=c2−a2,(a+b)(a−b)=a2−b2.(b+c)(b-c)=b^2-c^2, \quad (c+a)(c-a)=c^2-a^2, \quad (a+b)(a-b)=a^2-b^2.

Thus,

ln⁡(xb+cyc+aza+b)=k[(b2−c2)+(c2−a2)+(a2−b2)]=k⋅0=0.\ln\left(x^{b+c}y^{c+a}z^{a+b}\right)= k\left[(b^2-c^2)+(c^2-a^2)+(a^2-b^2)\right]=k\cdot0=0.

Therefore,

xb+cyc+aza+b=e0=1.x^{b+c}y^{c+a}z^{a+b}=e^0=1.