Question

If $\frac{a+\log_4 3}{a+\log_2 3}=\frac{a+\log_8 3}{a+\log_4 3}=b$, then b is equal to

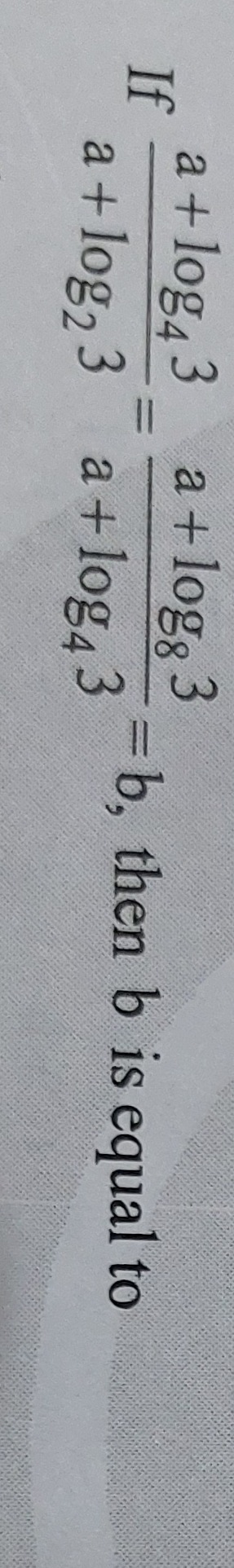
Answer 1

b = 1/3

Answer 2

We are given

$$\frac{a+\log_4 3}{a+\log_2 3}=\frac{a+\log_8 3}{a+\log_4 3}=b.$$

1. Express the logarithms in terms of $\log_2 3$ (let $L=\log_2 3$):

   • $\log_4 3=\frac{L}{2}$ because $\log_4 3=\frac{\log_2 3}{\log_2 4}=\frac{L}{2}$.
   • $\log_8 3=\frac{L}{3}$ because $\log_8 3=\frac{\log_2 3}{\log_2 8}=\frac{L}{3}$.

2. Substitute into the fractions:

   $$\frac{a+\frac{L}{2}}{a+L}=b \quad \Longrightarrow \quad a+\frac{L}{2}=b(a+L) \quad \Longrightarrow \quad a(1-b)=L\left(b-\frac{1}{2}\right).\tag{1}$$ $$\frac{a+\frac{L}{3}}{a+\frac{L}{2}}=b \quad \Longrightarrow \quad a+\frac{L}{3}=b\left(a+\frac{L}{2}\right) \quad \Longrightarrow \quad a(1-b)=L\left(\frac{b}{2}-\frac{1}{3}\right).\tag{2}$$

3. Equate the expressions for $a(1-b)$ from (1) and (2):

   $$L\left(b-\frac{1}{2}\right)=L\left(\frac{b}{2}-\frac{1}{3}\right).$$

   Cancel $L$ (since $L \neq 0$):

   $$b-\frac{1}{2}=\frac{b}{2}-\frac{1}{3}.$$

4. Multiply the entire equation by 6 to eliminate fractions:

   $$6b-3=3b-2.$$

   Solve for $b$:

   $$6b-3b= -2+3 \quad \Longrightarrow \quad 3b=1 \quad \Longrightarrow \quad b=\frac{1}{3}.$$

Therefore, $b=\frac{1}{3}$.