Question
Question: If $\frac{3}{2 + \cos \theta + i \sin \theta} = a + ib$, then prove that $a^2 + b^2 = 4a - 3$....
If 2+cosθ+isinθ3=a+ib, then prove that a2+b2=4a−3.
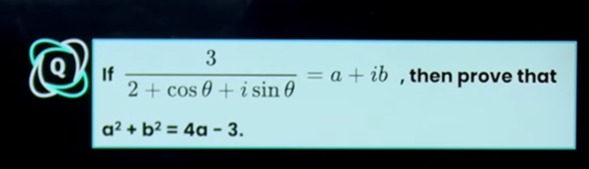
a^2 + b^2 = 4a - 3
Solution
The problem asks us to prove a relationship between a, b, and θ given a complex number equation.
Let the given equation be: 2+cosθ+isinθ3=a+ib Let z=cosθ+isinθ. We know that z is a complex number on the unit circle, so its modulus ∣z∣=cos2θ+sin2θ=1. An important property for complex numbers on the unit circle is that zˉ=z1.
The given equation can be written as: a+ib=2+z3
We need to prove a2+b2=4a−3.
Step 1: Express a2+b2 in terms of θ. We know that a2+b2=∣a+ib∣2. a2+b2=2+z32=∣2+z∣2∣3∣2=∣2+z∣29 Now, let's find ∣2+z∣2. For any complex number w, ∣w∣2=wwˉ. ∣2+z∣2=(2+z)(2+zˉ) Since ∣z∣=1, we have zˉ=z1. Substitute this into the expression: ∣2+z∣2=(2+z)(2+z1)=4+z2+2z+1=5+2(z+z1) Now substitute z=cosθ+isinθ and z1=cosθ−isinθ: z+z1=(cosθ+isinθ)+(cosθ−isinθ)=2cosθ So, ∣2+z∣2=5+2(2cosθ)=5+4cosθ Therefore, a2+b2=5+4cosθ9⋯(1)
Step 2: Express a in terms of θ. From a+ib=2+z3, we can find a by taking the real part: a=Re(2+z3) To find the real part, we multiply the numerator and denominator by the conjugate of the denominator: a=Re((2+z)(2+zˉ)3(2+zˉ))=Re(∣2+z∣23(2+zˉ)) Substitute ∣2+z∣2=5+4cosθ and zˉ=cosθ−isinθ: a=Re(5+4cosθ3(2+cosθ−isinθ)) The real part is: a=5+4cosθ3(2+cosθ)
Step 3: Express 4a−3 in terms of θ. Substitute the expression for a into 4a−3: 4a−3=4(5+4cosθ3(2+cosθ))−3 4a−3=5+4cosθ12(2+cosθ)−3 To combine these terms, find a common denominator: 4a−3=5+4cosθ12(2+cosθ)−3(5+4cosθ) 4a−3=5+4cosθ24+12cosθ−15−12cosθ 4a−3=5+4cosθ9⋯(2)
Step 4: Compare the results. From (1) and (2), we have: a2+b2=5+4cosθ9 4a−3=5+4cosθ9 Since both expressions are equal to 5+4cosθ9, we can conclude: a2+b2=4a−3 Hence, the proof is complete.
