Question

If $f(n) = \lim_{x \to 0} \left\{ \left(1 + \sin \frac{x}{2} \right) \left(1 + \sin \frac{x}{2^2} \right) ... \left(1 + \sin \frac{x}{2^n} \right) \right\}^{\frac{1}{x}}$ then find $\lim_{n \to \infty} f(n)$.

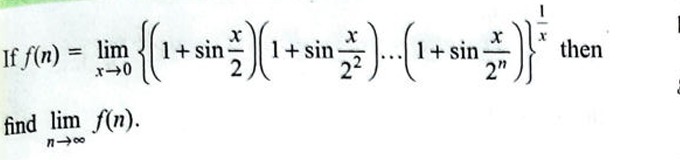
• A. e
• B. 1
• C. 0
• D. infinity

Answer 1

Answer: (A)

e

Answer 2

The limit $f(n)$ is evaluated by converting the $1^\infty$ indeterminate form to an exponential form $e^{\lim_{x \to 0} \frac{\ln(\text{product})}{x}}$. The logarithm of the product is expressed as a sum. Using Taylor series expansions for $\sin u$ and $\ln(1+u)$ for small $u$, we find that $\lim_{x \to 0} \frac{\ln(1+\sin(x/2^k))}{x} = \frac{1}{2^k}$. Summing these terms from $k=1$ to $n$ gives a geometric series, whose sum is $1 - (1/2)^n$. Thus, $f(n) = e^{1 - (1/2)^n}$. Finally, taking the limit as $n \to \infty$, since $(1/2)^n \to 0$, the limit becomes $e^1 = e$.