Solveeit Logo
Login

Question

Question: If $F(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0...

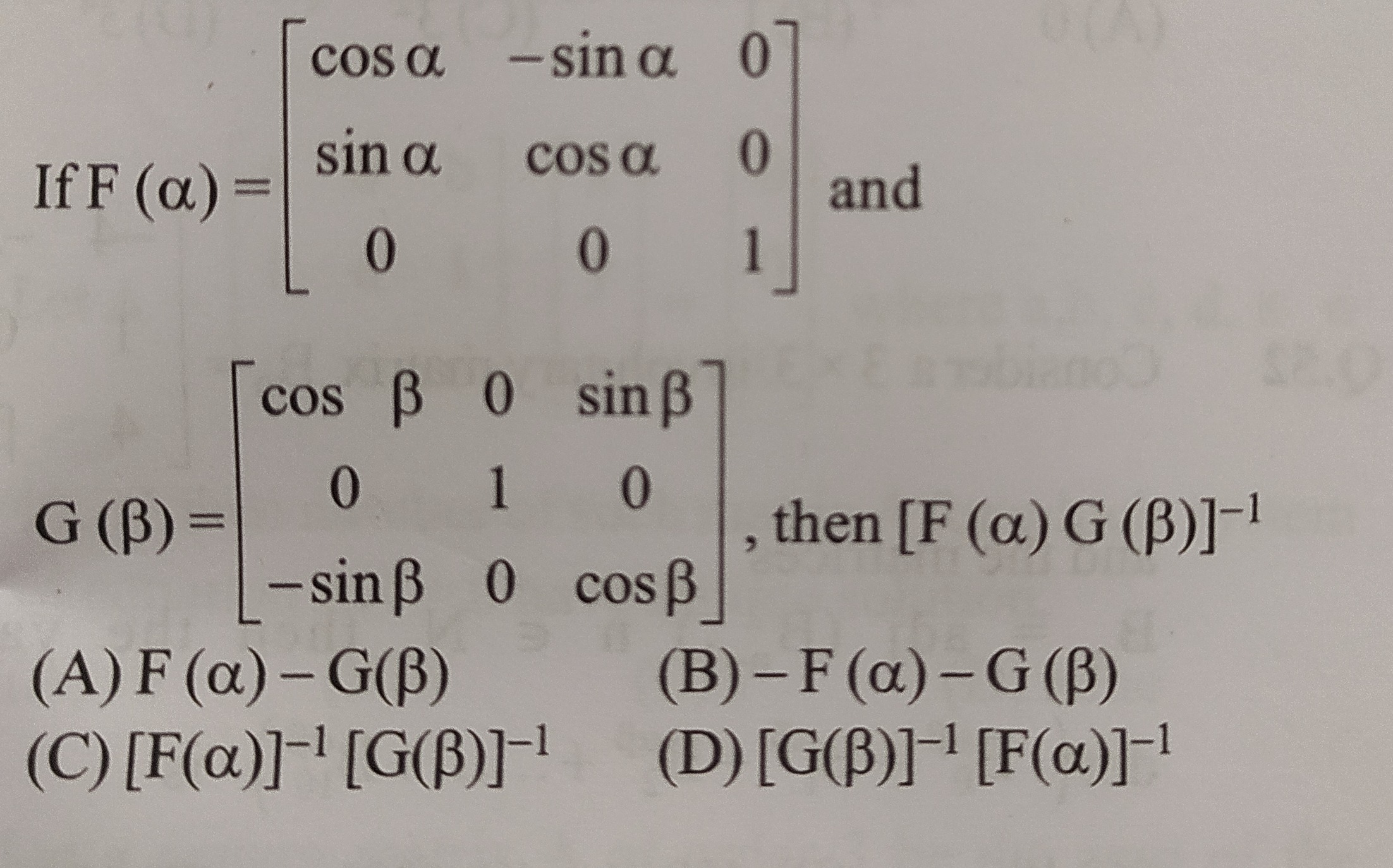
If F(α)=[cos⁡α−sin⁡α0sin⁡αcos⁡α0001]F(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} and G(β)=[cos⁡β0sin⁡β010−sin⁡β0cos⁡β]G(\beta) = \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{bmatrix}, then [F(α)G(β)]−1[F(\alpha)G(\beta)]^{-1}

A

F(α)−G(β)F(\alpha) - G(\beta)

B

−F(α)−G(β)-F(\alpha) - G(\beta)

C

[F(α)]−1[G(β)]−1[F(\alpha)]^{-1}[G(\beta)]^{-1}

D

[G(β)]−1[F(α)]−1[G(\beta)]^{-1}[F(\alpha)]^{-1}

Answer

(AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}

Explanation

Solution

The problem requires finding the inverse of the product of two matrices, F(α)F(\alpha) and G(β)G(\beta).

Key concept: The inverse of a product of matrices is the product of their inverses in reverse order. That is, for matrices A and B, (AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}.

Given F(α)F(\alpha) and G(β)G(\beta), we want to find [F(α)G(β)]−1[F(\alpha)G(\beta)]^{-1}. Applying the property of inverses, we have:

[F(α)G(β)]−1=[G(β)]−1[F(α)]−1[F(\alpha)G(\beta)]^{-1} = [G(\beta)]^{-1}[F(\alpha)]^{-1}

Therefore, the correct answer is [G(β)]−1[F(α)]−1[G(\beta)]^{-1}[F(\alpha)]^{-1}.