Question

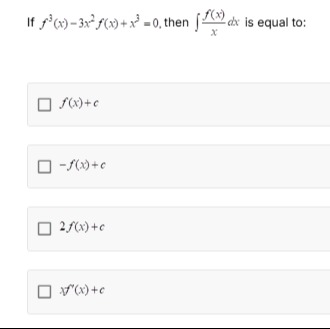
If $f^3(x)-3x^2f(x)+x^3=0$, then $\int \frac{f(x)}{x}dx$ is equal to:

• A. f(x)+c
• B. -f(x)+c
• C. 2f(x)+c
• D. xf'(x)+c

Answer 1

Answer: (A), (D)

f(x)+c, xf'(x)+c

Answer 2

The given equation is $f^3(x)-3x^2f(x)+x^3=0$. Dividing by $x^3$ (assuming $x \neq 0$), we get: $\left(\frac{f(x)}{x}\right)^3 - 3\left(\frac{f(x)}{x}\right) + 1 = 0$ Let $y(x) = \frac{f(x)}{x}$. Then $y(x)^3 - 3y(x) + 1 = 0$. If $f(x)$ is a differentiable function, then $y(x)$ must be a constant, say $k$, where $k$ is a root of $t^3 - 3t + 1 = 0$. Thus, $\frac{f(x)}{x} = k$, which implies $f(x) = kx$. Now, we compute the integral: $\int \frac{f(x)}{x}dx = \int \frac{kx}{x}dx = \int k \, dx = kx + c$ Since $f(x) = kx$, the integral is $f(x)+c$. Also, if $f(x) = kx$, then $f'(x) = k$. Therefore, $xf'(x)+c = x(k)+c = kx+c$. Both $f(x)+c$ and $xf'(x)+c$ are equal to $kx+c$.