Solveeit Logo
Login

Question

Question: If \(f(x) = x{e^{x(1 - x)}}\) then \(f(x)\) is: A. increasing on \(\left[ { - \dfrac{1}{2},1} \rig...

If f(x)=xex(1−x)f(x) = x{e^{x(1 - x)}} then f(x)f(x) is:
A. increasing on [−12,1]\left[ { - \dfrac{1}{2},1} \right]
B. decreasing on RR
C. increasing on RR
D. decreasing on [−12,1]\left[ { - \dfrac{1}{2},1} \right]

Explanation

Solution

For the increasing function it is that f′(x)f'(x) must be greater than zero and if it is less than zero then it would be the decreasing function. So first of all we need to find what the value of f′(x)f'(x) is.

Complete step by step solution:
Here we are given the function which is denoted by f(x)=xex(1−x)f(x) = x{e^{x(1 - x)}} and we need to find which interval it is increasing or decreasing. First of all we need to find the meaning of what is increasing and decreasing function. So let us explain it through an example like here we have the graph which is shown in the figure below.

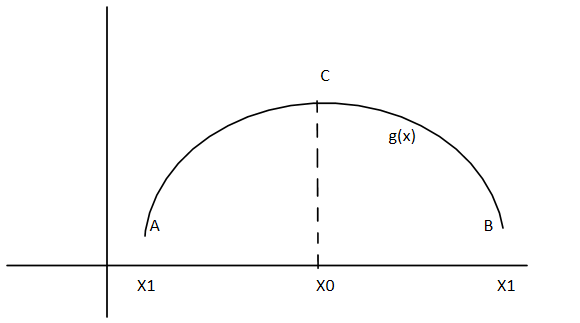
Here from A to CA{\text{ to }}C we see that the graph is increasing that is g(x1)<g(x0)g({x_1}) < g({x_0}) so we can say that in the interval (x1,x0)({x_1},{x_0}) graph of the function g(x)g(x) is increasing but from the range between x0 to x1{x_0}{\text{ to }}{x_1} it starts decreasing as the graph here now starts to fall downwards. So we can say that in the interval (x0,x1)({x_0},{x_1}) the function is decreasing. Now the basic point to know whether the graph is increasing or decreasing is that we first of all we need to find the derivative of that function. Then if it comes out to be positive then it is an increasing function but if it is negative then it is a decrease in that part of the range.
So here we are given the function which is
f(x)=xex(1−x)f(x) = x{e^{x(1 - x)}}
So upon differentiating we will get that
Here f(x)f(x) is given in the form of g(x)h(x)g(x)h(x)
So we get that f′(x)=g′(x)h(x)+h′(x)g(x)f'(x) = g'(x)h(x) + h'(x)g(x)
Here we get that
⇒g(x)=x ⇒h(x)=ex(1−x)=ex−x2 ⇒g′(x)=1 ⇒h′(x)=ex−x2.ddx(x−x2)=ex−x2(1−2x)  \Rightarrow g(x) = x \\\ \Rightarrow h(x) = {e^{x(1 - x)}} = {e^{x - {x^2}}} \\\ \Rightarrow g'(x) = 1 \\\ \Rightarrow h'(x) = {e^{x - {x^2}}}.\dfrac{d}{{dx}}(x - {x^2}) = {e^{x - {x^2}}}(1 - 2x) \\\
So we can write that
⇒f′(x)=1.ex−x2+x(1−2x)ex−x2 ⇒f′(x)=(1+x−2x2)ex−x2  \Rightarrow f'(x) = 1.{e^{x - {x^2}}} + x(1 - 2x){e^{x - {x^2}}} \\\ \Rightarrow f'(x) = (1 + x - 2{x^2}){e^{x - {x^2}}} \\\
We can write it as
f′(x)=−ex−x2(2x2−x+1) =−ex(1−x)(2x2−2x+x+1) =−ex(1−x)(2x(x−1)+1(x−1)) =−ex(1−x)(2x+1)(x−1)  f'(x) = - {e^{x - {x^2}}}(2{x^2} - x + 1) \\\ = - {e^{x(1 - x)}}(2{x^2} - 2x + x + 1) \\\ = - {e^{x(1 - x)}}(2x(x - 1) + 1(x - 1)) \\\ = - {e^{x(1 - x)}}(2x + 1)(x - 1) \\\
So we need to point out where f′(x)=0f'(x) = 0
⇒2x+1=0 ⇒x=−12 ⇒x−1=0 ⇒x=1  \Rightarrow 2x + 1 = 0 \\\ \Rightarrow x = - \dfrac{1}{2} \\\ \Rightarrow x - 1 = 0 \\\ \Rightarrow x = 1 \\\
Case 1
For x<\-12x < \- \dfrac{1}{2}
Let us put x=−1x = - 1
f′(−1)=−e−2(−2+1)(−2)=negativef'( - 1) = - {e^{ - 2}}( - 2 + 1)( - 2) = {\text{negative}}
So it is decreasing at x<\-12x < \- \dfrac{1}{2}
For −12<x<1 - \dfrac{1}{2} < x < 1
Let us take x=0x = 0
f′(0)=−e0(0+1)(0−1)=1=positivef'(0) = - {e^0}(0 + 1)(0 - 1) = 1 = {\text{positive}}
Hence it is increasing here for −12<x<1 - \dfrac{1}{2} < x < 1

So we can say that it is increasing in the interval [−12,1]\left[ { - \dfrac{1}{2},1} \right]

Note:
f′(x)f'(x) for any function represents to us the slope of that function at that point. If the slope is greater than 90∘90^\circ then it will be negative and if slope is less than 90∘90^\circ then value will be positive.