Question: If \( f(x) = \left\\{ {\begin{array}{*{20}{c}} {1,x < 0} \\\ {{x^2},x \geqslant 0} \end{...

Question

If $f(x) = \left\\{ {\begin{array}{*{20}{c}} {1,x < 0} \\\ {{x^2},x \geqslant 0} \end{array}} \right.$ then at $x = 0$
(A) $f'$ is differentiable
(B) $f$ is continuous.
(C) $f$ is differentiable
(D) $f$ is not continuous

Answer 1

Solution

Hint : Use the mathematical definition of continuity to check it at the given point. We can differentiate the function and then check if it gives the same value in both the parts of the function to check the differentiability.

Complete step-by-step answer :
In this question it is given that $f(x) = \left\\{ {\begin{array}{*{20}{c}} {1,x < 0} \\\ {{x^2},x \geqslant 0} \end{array}} \right.$
So we have to find the continuity of the function at $x = 0$
First we have to know when any $f(x)$ is continuous or discontinuous.
$\Rightarrow$ There are two limits,
Left hand limit ( $L.H.L$ ) and
Right hand limit ( $R.H.L$ )
If $L.H.L = R.H.L$
Then the limit of the function exists. We can check for continuity of the function, only if its limit exists.
If $L.H.L \ne R.H.L$
Then the limit of the function does not exist. And hence, the function will be discontinuous.
So, let’s start finding $L.H.L$ and $R.H.L$ .
For, $x < 0$ , then we put $(x - h)$ in function called $L.H.L$
Since, LHL is constant, there will be no change.
$\Rightarrow L.H.L = 1$
For, $x > 0$ put, $x + h$ in place of $x$ .
$\Rightarrow \mathop {\lim }\limits_{h \to 0} {\left( {0 + h} \right)^2} = R.H.L$
$\Rightarrow 0 = R.H.L$
Hence, $L.H.L \ne R.H.L$ .
So, the function $f(x) = \left\\{ {\begin{array}{*{20}{c}} {1,x < 0} \\\ {{x^2},x \geqslant 0} \end{array}} \right.$ is discontinuous at $x = 0$
By the definition of differentiability, a function can be differentiable, only if it is continuous. Therefore, the given function is not differentiable. Hence, clearly, $f'$ cannot be differentiable.
So, the correct answer is “Option D”.

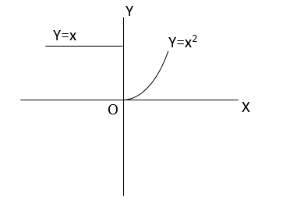
Note : Since discontinuous function cannot be differentiable, therefore options [A] and [C] are incorrect. You can also solve it by graph. From the graph, you can clearly observe that $f(x)$ is not continuous at $x = 0.$