Solveeit Logo
Login

Question

Question: If \(f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}\) where \(\left[ x \right]\) denotes the i...

If f(x)=2sin⁡3πx+x−[x]f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}} where [x]\left[ x \right] denotes the integral part of xx is a periodic function with the period.

Explanation

Solution

Hint: For f(x)f(x) to be periodic function so we know that a function f is periodic with period T if f(x+T)=f(x)f(x + T) = f(x) where TT is the period. We’ll also use the property of the greatest integer function that is x−[x]=xx - [x] = \\{ x\\} and its period is 1.

Complete step by step solution:
Here we are given the function which is defined as f(x)=2sin⁡3πx+x−[x]f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}} where [x]\left[ x \right] denotes the integral part. We need to find the period of this function. Given that the function is periodic now we need to know what the periodic function means. So periodic function is the function which repeats its value after the regular interval. For example any trigonometric function repeats its value after the interval 2π2\pi . Periodic function can be easily determined by using the graph. So for the periodic function it must follow that f(x+T)=f(x)f(x + T) = f(x) where TT represents the period. Now if we are given the function
f(x)=2sin⁡3πx+x−[x]f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}
We need to find the period of the function sin⁡3πx{\sin ^3}\pi x and x−[x]x - [x]
So let us suppose that g(x)=x−[x]g(x) = x - [x]
Now if we take g(x+T)=x+T−[x+T]g(x + T) = x + T - [x + T]
Now we know that x−[x]=xx - [x] = \\{ x\\}
Here x\\{ x\\} is the fractional part of xx whose graph is given by

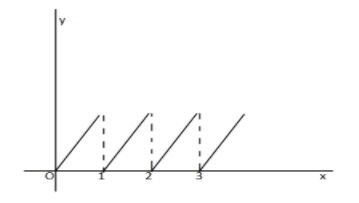
So as we see the graph is similar in [0,1),[1,2),...and so on[0,1),[1,2),...{\text{and so on}}
Hence we can say that g(x+1)=g(x)g(x + 1) = g(x)
Therefore the period of x−[x]=xx - [x] = \\{ x\\} is 11
For sin⁡3πx{\sin ^3}\pi x if we replace x→x+2x \to x + 2
Then we can write as sin⁡3π(x+2){\sin ^3}\pi (x + 2)
Which is (sin⁡(2π+πx))3{(\sin (2\pi + \pi x))^3}
And we know that sin⁡(2π+θ)=sin⁡θ\sin (2\pi + \theta ) = \sin \theta
If we take h(x)=sin⁡3πxh(x) = {\sin ^3}\pi x
h(x+2)=sin⁡3(2π+πx)h(x + 2) = {\sin ^3}(2\pi + \pi x)
=sin⁡3πx= {\sin ^3}\pi x
⇒h(x+2)=h(x)\Rightarrow h(x + 2) = h(x)
Therefore its period is 22
Now for finding the period of sin⁡3πx+x−[x]{\sin ^3}\pi x + x - [x]
We need to take the LCM of 1,21,2 which is 22
And as we have the function f(x)=2sin⁡3πx+x−[x]f(x) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}}
sin⁡3πx+x−[x]{\sin ^3}\pi x + x - [x] has the period 22
So f(x)f(x) has the period 22
As we can find f(x+2)f(x + 2)
f(x+2)=2sin⁡3π(x+2)+x+2−[x+2] ⇒f(x+2)=2sin⁡3(2π+πx)+x+2−[x]−2  f(x + 2) = {2^{{{\sin }^3}\pi (x + 2) + x + 2 - \left[ {x + 2} \right]}} \\\ \Rightarrow f(x + 2) = {2^{{{\sin }^3}(2\pi + \pi x) + x + 2 - [x] - 2}} \\\
⇒f(x+2)=2sin⁡3πx+x−[x]\Rightarrow f(x + 2) = {2^{{{\sin }^3}\pi x + x - \left[ x \right]}} =f(x) = f(x)

So, the period of f(x)f(x) is 22.

Note:
If f(x)f(x) is periodic with the period TT then we can write that f(x+nT)=f(x)f(x + nT) = f(x)
We can also write that f(x+2T)=f(x+T)=f(x)f(x + 2T) = f(x + T) = f(x) and so on
All the trigonometric function have the period 2π2\pi
For example for sin⁡x\sin x
f(x+2π)=sin⁡(x+2π)=sin⁡x=f(x)f(x + 2\pi ) = \sin (x + 2\pi ) = \sin x = f(x)
So 2π2\pi is the period.