Question
Question: If $f: R \rightarrow R^+$ is differentiable function such that $|f(y) \cdot f(x-y) + (x-y)^2| \geq |...
If f:R→R+ is differentiable function such that ∣f(y)⋅f(x−y)+(x−y)2∣≥∣f(x)f(x−y)∣∀x,y∈R, f(0)=5, then the value of f(5) is
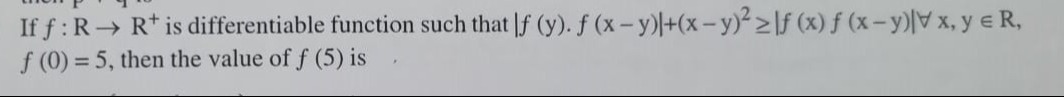
5
Solution
Let the given inequality be ∣f(y)⋅f(x−y)+(x−y)2∣≥∣f(x)f(x−y)∣ for all x,y∈R. We are given that f:R→R+ is a differentiable function, which means f(z)>0 for all z∈R. Since f(x−y)>0, we have ∣f(x−y)∣=f(x−y). We can divide both sides by f(x−y): ∣f(y)+f(x−y)(x−y)2∣≥∣f(x)∣. Since f(x)>0, ∣f(x)∣=f(x). ∣f(y)+f(x−y)(x−y)2∣≥f(x). Since f(y)>0 and (x−y)2≥0 and f(x−y)>0, the term f(y)+f(x−y)(x−y)2 is always non-negative. So, ∣f(y)+f(x−y)(x−y)2∣=f(y)+f(x−y)(x−y)2. The inequality simplifies to f(y)+f(x−y)(x−y)2≥f(x) for all x,y∈R.
This inequality must hold for all x,y∈R. Let's consider specific values for y. Case 1: Let y=x. Substituting y=x into the inequality, we get f(x)+f(x−x)(x−x)2≥f(x), which simplifies to f(x)+0≥f(x), or f(x)≥f(x). This is always true and provides no specific information about f(x).
Case 2: Let y=0. Substituting y=0 into the inequality, we get f(0)+f(x−0)(x−0)2≥f(x), which simplifies to f(0)+f(x)x2≥f(x) for all x∈R. We are given f(0)=5. So, 5+f(x)x2≥f(x) for all x∈R.
Let's rearrange this inequality: 5≥f(x)−f(x)x2 5≥f(x)[f(x)]2−x2. Since f(x)>0, we can multiply by f(x) without changing the direction of the inequality: 5f(x)≥[f(x)]2−x2 [f(x)]2−5f(x)−x2≤0 for all x∈R.
Let's consider the original inequality f(y)+f(x−y)(x−y)2≥f(x) again. Let x be fixed. Consider the function g(y)=f(y)+f(x−y)(x−y)2. The inequality states that g(y)≥f(x) for all y. This means that the minimum value of g(y) with respect to y is greater than or equal to f(x). If the minimum of g(y) occurs at some point y0, then g′(y0)=0. Let's calculate g′(y): g′(y)=dyd(f(y)+f(x−y)(x−y)2). Using the chain rule for the second term, let u=x−y, so dydu=−1. dyd(f(x−y)(x−y)2)=dud(f(u)u2)dydu=([f(u)]22uf(u)−u2f′(u))(−1) =−[f(x−y)]22(x−y)f(x−y)−(x−y)2f′(x−y)=[f(x−y)]2(x−y)2f′(x−y)−2(x−y)f(x−y). So, g′(y)=f′(y)+[f(x−y)]2(x−y)2f′(x−y)−2(x−y)f(x−y).
Consider the specific point y=x. g(x)=f(x)+f(x−x)(x−x)2=f(x)+f(0)0=f(x). Since g(y)≥f(x) for all y, and g(x)=f(x), this implies that y=x is a point where the function g(y) attains its minimum value, which is exactly f(x). For y=x to be a minimum point, the derivative g′(y) must be zero at y=x. g′(x)=f′(x)+[f(x−x)]2(x−x)2f′(x−x)−2(x−x)f(x−x)=f′(x)+[f(0)]20⋅f′(0)−0⋅f(0)=f′(x)+0=f′(x). Since y=x is the minimum point, g′(x) must be zero. g′(x)=0⟹f′(x)=0 for all x∈R.
If f′(x)=0 for all x∈R, then f(x) must be a constant function. Let f(x)=c. Since f(0)=5, the constant must be c=5. So, f(x)=5.
Let's verify if f(x)=5 satisfies all the given conditions.
- f:R→R+: f(x)=5 maps R to {5}, which is a subset of R+. This is satisfied.
- f is differentiable: f(x)=5 is a constant function, and its derivative f′(x)=0 exists for all x∈R. This is satisfied.
- f(0)=5: f(0)=5 is given and satisfied by f(x)=5.
- ∣f(y)⋅f(x−y)+(x−y)2∣≥∣f(x)f(x−y)∣ for all x,y∈R: Substitute f(x)=5 into the inequality: ∣5⋅5+(x−y)2∣≥∣5⋅5∣ ∣25+(x−y)2∣≥∣25∣ ∣25+(x−y)2∣≥25. Since (x−y)2≥0, 25+(x−y)2≥25. The term 25+(x−y)2 is always non-negative, so ∣25+(x−y)2∣=25+(x−y)2. The inequality becomes 25+(x−y)2≥25, which simplifies to (x−y)2≥0. This is true for all x,y∈R. So, f(x)=5 satisfies the given inequality for all x,y∈R.
Since f(x)=5 is the unique function satisfying the given conditions, we can find f(5). f(5)=5.
