Question

If f : R → R, f(x) = $\frac{2x^2 - 5x + 3}{8x^2 + 9x + 11}$, then f is -

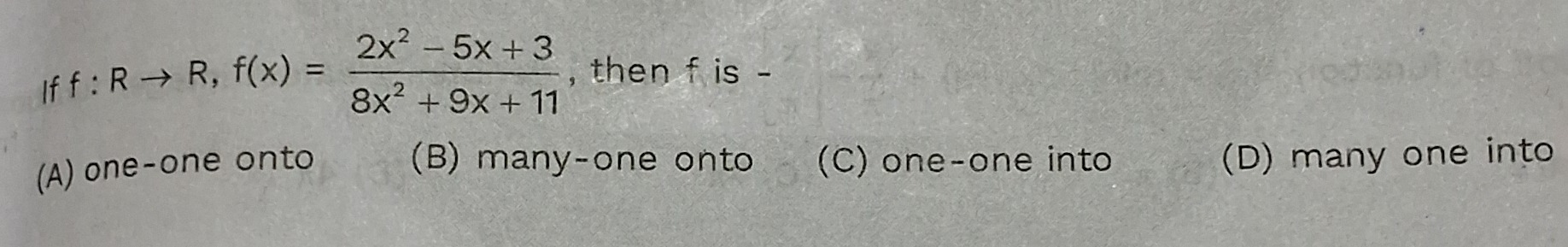
• A. one-one onto
• B. many-one onto
• C. one-one into
• D. many one into

Answer 1

Answer: (D)

many one into

Answer 2

The function is given by $f(x) = \frac{2x^2 - 5x + 3}{8x^2 + 9x + 11}$. The domain is $R$ and the codomain is $R$.

To determine if the function is one-one or many-one, we examine its derivative. $f'(x) = \frac{(4x - 5)(8x^2 + 9x + 11) - (2x^2 - 5x + 3)(16x + 9)}{(8x^2 + 9x + 11)^2}$

The numerator simplifies to $58x^2 - 4x - 82$. The denominator is $(8x^2 + 9x + 11)^2$. The quadratic $8x^2 + 9x + 11$ has discriminant $9^2 - 4(8)(11) = 81 - 352 = -271 < 0$. Since the leading coefficient is positive, $8x^2 + 9x + 11 > 0$ for all real $x$. Thus, the denominator $(8x^2 + 9x + 11)^2$ is always positive.

The sign of $f'(x)$ is determined by the sign of the numerator $58x^2 - 4x - 82$. The discriminant of $58x^2 - 4x - 82$ is $(-4)^2 - 4(58)(-82) = 16 + 19024 = 19040 > 0$. Since the discriminant is positive, the quadratic $58x^2 - 4x - 82$ has two distinct real roots. Let these roots be $x_1$ and $x_2$. The quadratic changes sign at these roots.

Since $f'(x)$ changes sign, the function $f(x)$ is not strictly monotonic on $R$. Therefore, $f(x)$ is a many-one function.

To determine if the function is onto or into, we find the range of the function. Let $y = f(x)$. $y = \frac{2x^2 - 5x + 3}{8x^2 + 9x + 11}$ $y(8x^2 + 9x + 11) = 2x^2 - 5x + 3$ $(8y - 2)x^2 + (9y + 5)x + (11y - 3) = 0$

For the range, we need to find the values of $y$ for which this quadratic equation in $x$ has real solutions. If $8y - 2 \neq 0$, the discriminant must be non-negative: $D = (9y + 5)^2 - 4(8y - 2)(11y - 3) \ge 0$ $D = (81y^2 + 90y + 25) - 4(88y^2 - 46y + 6)$ $D = 81y^2 + 90y + 25 - 352y^2 + 184y - 24$ $D = -271y^2 + 274y + 1 \ge 0$ $271y^2 - 274y - 1 \le 0$

The roots of $271y^2 - 274y - 1 = 0$ are $y = \frac{274 \pm \sqrt{(-274)^2 - 4(271)(-1)}}{2(271)} = \frac{274 \pm \sqrt{75076 + 1084}}{542} = \frac{274 \pm \sqrt{76160}}{542}$. Let $y_1 = \frac{274 - \sqrt{76160}}{542}$ and $y_2 = \frac{274 + \sqrt{76160}}{542}$. Since the parabola $271y^2 - 274y - 1$ opens upwards, the inequality $271y^2 - 274y - 1 \le 0$ holds for $y_1 \le y \le y_2$.

If $8y - 2 = 0$, i.e., $y = \frac{1}{4}$, the equation becomes a linear equation: $(9(\frac{1}{4}) + 5)x + (11(\frac{1}{4}) - 3) = 0$, which gives $\frac{29}{4}x - \frac{1}{4} = 0$, so $x = \frac{1}{29}$. This is a real solution, so $y = \frac{1}{4}$ is in the range. We check if $y = \frac{1}{4}$ lies in the interval $[y_1, y_2]$ by substituting it into $271y^2 - 274y - 1$: $271(\frac{1}{4})^2 - 274(\frac{1}{4}) - 1 = \frac{271}{16} - \frac{274}{4} - 1 = \frac{271 - 1096 - 16}{16} = \frac{-841}{16} \le 0$. So $y = \frac{1}{4}$ is in the interval.

The range of the function is the closed interval $[y_1, y_2]$. The codomain of the function is $R$. Since the range $[y_1, y_2]$ is a proper subset of the codomain $R$ (a closed interval is not equal to $R$), the function is into.

Combining the results, the function is many-one and into.