Question

If $f\left( x \right) = \dfrac{x}{{{x^2} + 1}}$is increasing function then the value of x lies in the
${\text{A}}{\text{. }}R \\\ {\text{B}}{\text{. }}\left( { - \infty ,1} \right) \\\ {\text{C}}{\text{. }}\left( {1,\infty } \right) \\\ {\text{D}}{\text{. }}\left( { - 1,1} \right) \\\$

Answer 1

Here we go through the properties of increasing and decreasing function as we know that when a function is increasing in nature then its first derivative is greater than zero.

Complete step-by-step answer:
Here in the question it is given that
$f\left( x \right) = \dfrac{x}{{{x^2} + 1}}$Is an increasing function
We know that if a function is increasing in nature that means its first derivative should be greater than zero.
i.e. $f'\left( x \right) > 0$
Now for solving the question we have to find out the first derivative of the given function.
Here the function is in the form of fraction so we apply the divisibility rule of derivative that we learn in differentiation chapter.
$\Rightarrow f'\left( x \right) = \dfrac{{\dfrac{{d(x)}}{{dx}}\left( {{x^2} + 1} \right) - \dfrac{{d\left( {{x^2} + 1} \right)}}{{dx}}(x)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\\ \Rightarrow f'\left( x \right) = \dfrac{{\left( {{x^2} + 1} \right)(1) - x\left( {2x} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\\ \Rightarrow f'\left( x \right) = \dfrac{{{x^2} + 1 - 2{x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\\ \Rightarrow f'\left( x \right) = \dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\\$
Now given that f(x) is increasing function.
It means $f'\left( x \right) > 0$
i.e. $\dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0$
Now we can clearly see that ${\left( {{x^2} + 1} \right)^2}$ is always positive because of its square.
Or ${\left( {{x^2} + 1} \right)^2} > 0$
So for $f'\left( x \right) > 0$ we have to say $1 - {x^2} > 0$ ($\because$denominator is always positive and to make whole term positive numerator must be positive)
i.e. $\left( {1 - x} \right)\left( {1 + x} \right) > 0$
Now we represent it on number line we get,

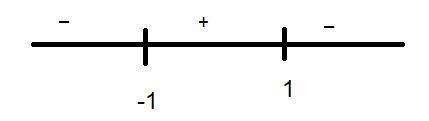
$\Rightarrow - 1 < x < 1$
Or x lies in (-1, 1).

So, the correct answer is “Option D”.

Note: Whenever we face such a type of question the key concept for solving the question is always try to find out the derivative of the function when it is the question about the nature of the function either it is increasing or decreasing as we know that whenever a function is increasing then its derivative must be positive.