Question

If $f\left( x \right)=2{{x}^{2}}+5$ and $g\left( x \right)=3x+a$, how do you find a so that the graph of $f\left( g\left( x \right) \right)$ crosses the y-axis at 23?

Answer 1

We first find the composite function $f\left( g\left( x \right) \right)$. Then we find the Y-axis intercept by putting the value of $x=0$. We solve it to find the value of a. It is given that the Y intercept is 23.

Complete step by step solution:
It is given that $f\left( x \right)=2{{x}^{2}}+5$ and $g\left( x \right)=3x+a$. We first have to find the composite function of $f\left( g\left( x \right) \right)$.
Therefore, $f\left( g\left( x \right) \right)=f\left( 3x+a \right)=2{{\left( 3x+a \right)}^{2}}+5$.
Now we have to find the value of a so that the graph of $f\left( g\left( x \right) \right)$ crosses the y-axis at 23.
We assume $y=f\left( g\left( x \right) \right)=2{{\left( 3x+a \right)}^{2}}+5$.
This means we first find the Y-axis intercepts. In that case for Y-axis, we have to take the coordinate values of x as 0. Putting the value of $x=0$ in the equation $y=2{{\left( 3x+a \right)}^{2}}+5$, we get
$\begin{aligned} & y=2{{\left( 3x+a \right)}^{2}}+5 \\\ & \Rightarrow y=2{{\left( 3\times 0+a \right)}^{2}}+5=2{{a}^{2}}+5 \\\ \end{aligned}$
It is given the value of y will be 23.
This gives $2{{a}^{2}}+5=23$. We solve the quadratic to find the value of a.
We need to find the solution of the given equation $2{{a}^{2}}-18=0$.
First, we divide both sides of the equation by 2 and get $\dfrac{2{{a}^{2}}-18}{2}=0\Rightarrow {{a}^{2}}-9=0$.
Now we have a quadratic equation ${{a}^{2}}-9=0$ which gives ${{a}^{2}}-{{3}^{2}}=0$.
Now we find the factorisation of the equation ${{a}^{2}}-{{3}^{2}}=0$ using the identity of ${{x}^{2}}-{{y}^{2}}=\left( x+y \right)\left( x-y \right)$.
Therefore, we get
$\begin{aligned} & {{a}^{2}}-{{3}^{2}}=0 \\\ & \Rightarrow \left( a+3 \right)\left( a-3 \right)=0 \\\ \end{aligned}$
We get the values of a as either $\left( a+3 \right)=0$ or $\left( a-3 \right)=0$.
This gives $a=-3,3$.

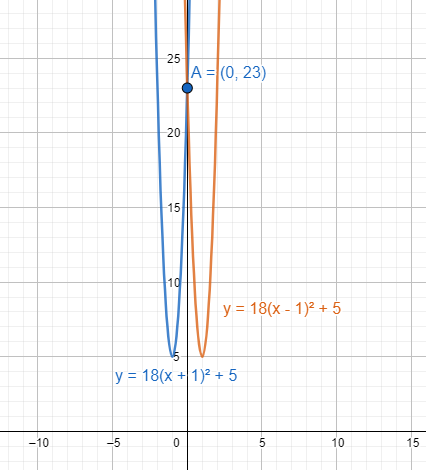
Note: We can also apply the quadratic equation formula to solve the equation $2{{a}^{2}}-18=0$.
We know for a general equation of quadratic $a{{x}^{2}}+bx+c=0$, the value of the roots of x will be $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$.
In the given equation we have $2{{a}^{2}}-18=0$. The values of coefficients are $2,0,-18$ respectively.
We put the values and get a as $a=\dfrac{-0\pm \sqrt{{{0}^{2}}-4\times 2\times \left( -18 \right)}}{2\times 2}=\dfrac{\pm \sqrt{144}}{4}=\dfrac{\pm 12}{4}=\pm 3$.