Question
Question: If f is defined on an interval [a,b], which of the following is/are incorrect: [a] If f(a) and f(b...
If f is defined on an interval [a,b], which of the following is/are incorrect:
[a] If f(a) and f(b) are of opposite sign, then there must exist a point c in (a,b) such that f(c) = 0
[b] If f is continuous on [a,b], f(a)<0 and f(b)<0, then there must exist a point c in (a,b) such that f(x) = 0
[c] If f is continuous on [a,b] and there is a point c in (a,b) such that f(c) = 0, the f(a) and f(b) must be of opposite sign.
[d] If f has no zeros on [a,b], then f(a) and f(b) have the same sign
Solution
Hint: Use Intermediate value theorem in option [b]. In option [a] take f(x)=x1 and a = -1 and b = 1. Hence argue that the statement is incorrect. For option [c] take f(x)=x2 and a =-1, b = 1 and c= 0. Hence argue why the statement is incorrect. For option [d] again take f(x)=x1 and a = -1 and b = 1. Hence argue that the statement is incorrect.
Complete step-by-step answer:
When we prove that a statement is correct, we need to come up with formal proof, and when we prove that a statement is incorrect, we come with a counterexample(Proof by counterexample).
In the question above, we will argue that the statements a,c and d are incorrect, whereas statement b is correct. We will come up with counterexamples disproving statements a,c and d and we will prove the correctness of the statement in option [b].
Proving that statement [a] is incorrect:
Consider the function f(x)=x1, in the interval [−1,1].
We have f(−1)=−1<0 and f(1)=1>0.
However if f(x) = 0, we have 1 = 0, which is not possible.
Hence we have f(1), and f(-1) have opposite signs, but there exists no c in (-1,1) such that f(c) = 0. Hence the given statement is incorrect.
Proving the correctness of statement [b]:
Intermediate Value theorem: According to intermediate value theorem if f(x) is a continuous function in the interval [a,b], then for all y lying between f(a) and f(b), there exists c∈(a,b) such that f(c)=y.
Since f is continuous in the interval [a,b] and f(a)<0,f(b)>0, we have 0∈(f(a),f(b))
Hence by Intermediate Value theorem, there exists c∈(a,b) such that f(c) = 0. Hence the statement is correct.
Proving that the statement [c] is incorrect:
Consider f(x)=x2.
Since f(x) is a polynomial and since every polynomial is continuous in R, we have f(x) is continuous in the interval [-1,1].
Clearly, there exists c=0∈(−1,1) such that f(c)=0, but f(1)>0 and f(−1)>0 and hence f(1) and f(-1) have the same sign.
Hence statement [c] is incorrect.
Proving that the statement [d] is incorrect:
Consider f(x)=x1.
Clearly, f(x) has no zeros in R , and hence f(x) has no zeros in [−1,1]. But f(1)>0 and f(−1)>0 and hence have opposite signs. Hence option [d] is incorrect.
Hence only options [a],[c] and [d] are incorrect.
Note:[1] Visualising graphically:
Graph of f(x)=x1
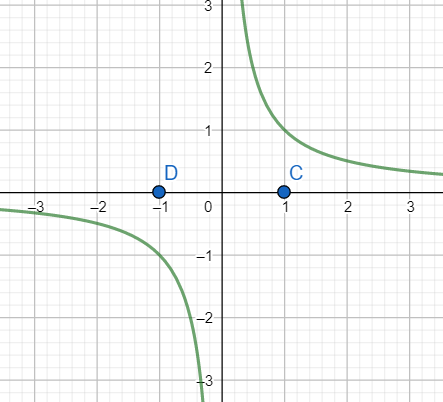
As is evident from the graph that in the interval [C, D] f(x) takes both negative values, but has no zeros. Hence options [a] and [d] are incorrect.
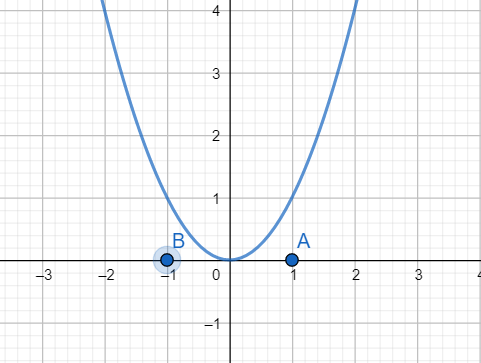
As evident from the graph of f(x)=x2, that f(A) and f(B) are of the same sign. But there exists a root of f(x) in the interval [B, A]
When we draw a continuous graph from x = a to x = b, our hand should not get raised from the paper while plotting. In other words, we can draw a continuous graph, not raising our hand until the graph is complete. Now if f(a) and f(b) are of opposite signs, (a,f(a)) and (b,f(b)) are on opposite sides of the x-axis, and hence when we draw the graph we need to cross the x-axis at least once in the interval (a,b) since we cannot raise our hand(Try it yourself once) and hence there exists c in the interval (a,b) such that f(c) = 0, which proves the statement [b] is correct.
