Question

If $f,g:R \to R$ be defined respectively by$f(x) = x + 1$and $g(x) = 2x - 3$, find $f + g$,$f - g$and, $\dfrac{f}{g}$

Answer 1

As the functions $f\left( x \right)$and$\;g\left( x \right)$are defined in R then their addition and subtraction functions will also be defined in R, but for their division function first we’ll define the domain for the function in the denominator, then will after dividing we’ll get the value of the function.

Complete step-by-step answer:
Given data: $f,g:R \to R$
$f(x) = x + 1$
$g(x) = 2x - 3$
We know that the function $f\left( x \right)$ and $\;g\left( x \right)$ are defined in R, i.e., the domain of both the functions is complete set R.
So the addition and the subtraction operation are possible for f and g
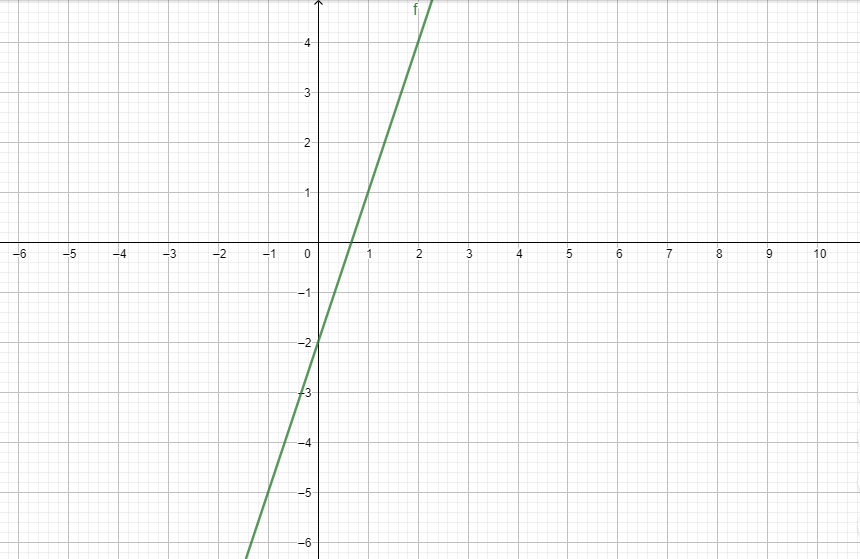
Therefore, $(f + g)(x) = x + 1 + 2x - 3$
$= 3x - 2$
$\therefore (f + g)(x) = 3x - 2$
And it is defined in R
i.e. the domain of $(f + g)(x) = ( - \infty ,\infty )$
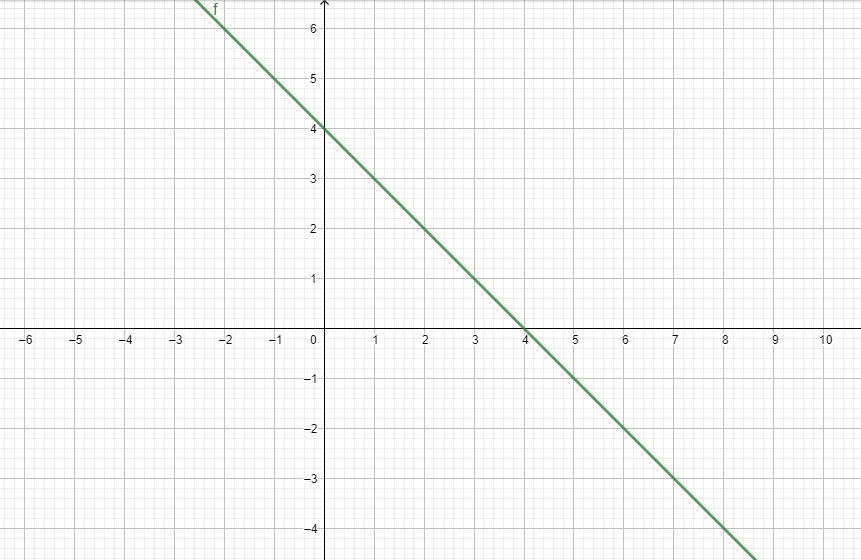
And, $(f - g)(x) = x + 1 - (2x - 3)$
$= x + 1 - 2x + 3$
$\therefore (f - g)(x) = 4 - x$
And it is defined in R
i.e. the domain of $(f - g)(x) = ( - \infty ,\infty )$
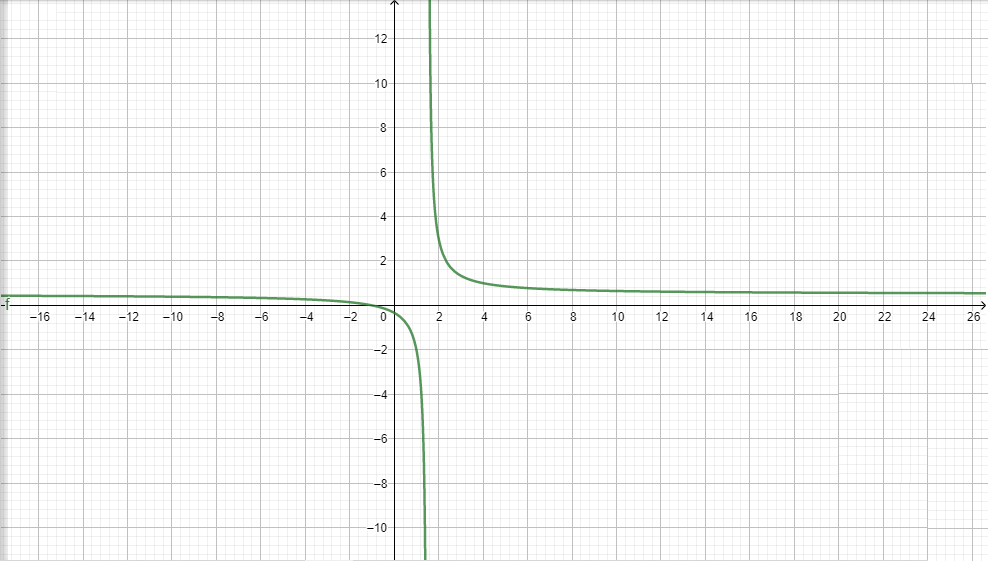
Now if we have to find $\dfrac{f}{g}$then$g(x) \ne 0$
i.e. $2x - 3 \ne 0$
adding 3 both sides
$\Rightarrow 2x \ne 3$
Dividing 2 into both sides
$\Rightarrow x \ne \dfrac{3}{2}$
therefore$\dfrac{f}{g}(x)$will be defined in R - \left\\{ {\dfrac{3}{2}} \right\\}
i.e. the domain of$\dfrac{f}{g}(x) = ( - \infty ,\dfrac{3}{2}) \cup (\dfrac{3}{2},\infty )$
the values of $\dfrac{f}{g}(x) = \dfrac{{x + 1}}{{2x - 3}}$

Note: Remember to find the domain of the function.
In the above solution, we have also mentioned the domain of the resulting functions i.e. $f + g$,$f - g$and, $\dfrac{f}{g}$, we can also show those in the graphical form as
$(f + g)(x) = 3x - 2$

$(f - g)(x) = 4 - x$

$\dfrac{f}{g}(x) = \dfrac{{x + 1}}{{2x - 3}}$