Question

If $f: A \rightarrow B$, where $A = \{a, b, c, d\}$ and $B = \{x, y, z\}$ and $f(a) = x$, then number of such INTO functions is

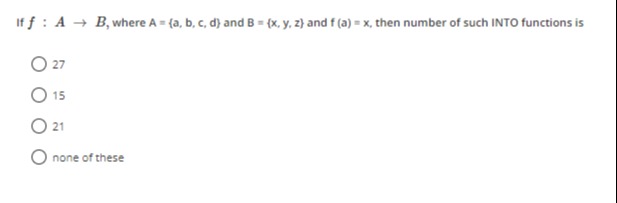
• A. 27
• B. 15
• C. 21
• D. none of these

Answer 1

Answer: (B)

15

Answer 2

To find the number of INTO functions from set A to set B with the given condition, we can use two approaches:

Approach 1: Total functions - ONTO functions

1. Calculate the total number of functions: Given $A = \{a, b, c, d\}$ and $B = \{x, y, z\}$. The condition is $f(a) = x$. This means the image of 'a' is fixed. For the remaining elements in A, i.e., $\{b, c, d\}$, each can be mapped to any of the 3 elements in B ({x, y, z}). Number of choices for $f(b)$ = 3 Number of choices for $f(c)$ = 3 Number of choices for $f(d)$ = 3 Total number of functions = $1 \times 3 \times 3 \times 3 = 3^3 = 27$.

2. Calculate the number of ONTO functions: An ONTO function means that every element in the codomain B must be the image of at least one element in the domain A. Since $f(a) = x$, the element 'x' in B is already covered. For the function to be ONTO, the remaining elements in B, i.e., $\{y, z\}$, must be covered by the images of the remaining elements in A, i.e., $\{b, c, d\}$. Let $A' = \{b, c, d\}$ and $B = \{x, y, z\}$. We need to find the number of functions $g: A' \rightarrow B$ such that $y \in g(A')$ and $z \in g(A')$.

   We use the Principle of Inclusion-Exclusion for this:

   • Total functions from $A'$ to $B$ is $3^{|A'|} = 3^3 = 27$.
   • Let $P_y$ be the property that 'y' is not in the range of $g(A')$. This means $g(A') \subseteq \{x, z\}$. The number of such functions is $2^3 = 8$.
   • Let $P_z$ be the property that 'z' is not in the range of $g(A')$. This means $g(A') \subseteq \{x, y\}$. The number of such functions is $2^3 = 8$.
   • Let $P_y \cap P_z$ be the property that 'y' and 'z' are not in the range of $g(A')$. This means $g(A') \subseteq \{x\}$. The number of such functions is $1^3 = 1$.

   The number of functions where 'y' is not covered OR 'z' is not covered is $|P_y \cup P_z| = |P_y| + |P_z| - |P_y \cap P_z| = 8 + 8 - 1 = 15$. The number of functions where both 'y' AND 'z' are covered by $f(\{b, c, d\})$ is: Total functions from $A'$ to $B$ - (Functions where y or z is not covered) $= 27 - 15 = 12$. These 12 functions, combined with $f(a)=x$, ensure that all elements of B are covered. Thus, there are 12 ONTO functions.

3. Calculate the number of INTO functions: An INTO function is a function that is not ONTO. Number of INTO functions = Total functions - Number of ONTO functions Number of INTO functions = $27 - 12 = 15$.

Approach 2: Direct calculation of INTO functions

An INTO function means the range of $f$, $f(A)$, is a proper subset of $B$. Since $f(a) = x$, 'x' must be in the range of $f$. So, the possible ranges for INTO functions are subsets of $B$ that contain $x$ but are not equal to $B$:

1. Range is $\{x\}$
2. Range is $\{x, y\}$
3. Range is $\{x, z\}$

• Case 1: $f(A) = \{x\}$ This means all elements of A must map to 'x'. Since $f(a)=x$ is given, we need $f(b)=x$, $f(c)=x$, $f(d)=x$. Number of functions = $1 \times 1 \times 1 = 1$.

• Case 2: $f(A) = \{x, y\}$ This means the elements $\{b, c, d\}$ must map to $\{x, y\}$ such that 'y' is in the range of $f(\{b, c, d\})$. Total functions from $\{b, c, d\}$ to $\{x, y\}$ is $2^3 = 8$. From these, we must exclude functions where 'y' is not in the range (i.e., all elements map to 'x'). The number of such functions is $1^3 = 1$. Number of functions for this case = $8 - 1 = 7$.

• Case 3: $f(A) = \{x, z\}$ This means the elements $\{b, c, d\}$ must map to $\{x, z\}$ such that 'z' is in the range of $f(\{b, c, d\})$. Total functions from $\{b, c, d\}$ to $\{x, z\}$ is $2^3 = 8$. From these, we must exclude functions where 'z' is not in the range (i.e., all elements map to 'x'). The number of such functions is $1^3 = 1$. Number of functions for this case = $8 - 1 = 7$.

Total number of INTO functions = (Case 1) + (Case 2) + (Case 3) = $1 + 7 + 7 = 15$.

Both approaches yield the same result.