Question
Question: If events A and B are independent and \(P\left( A \right)=0.15,P\left( A\cup B \right)=0.45\) then \...
If events A and B are independent and P(A)=0.15,P(A∪B)=0.45 then P(B)=
(a)136
(b)176
(c)196
(d)236
Solution
Hint: Two events A and B will be independent events of the relation between P(A) and P(B) is given as P(A∩B)=P(A)P(B) .
Now, use the relation among P(A),P(B),P(A∩B) and P(A∪B), which is given as:
P(A∪B)=P(A)+P(B)−P(A∩B) .
Now, put all the known values to the above equation to get the value of P(B) .
Complete step-by-step answer:
Here, we are given that A and B are two independent events with the relations
P(A)=0.15 ………………… (1)
P(A∪B)=0.45………………. (2)
And hence, we need to determine the value of P(B).
Now, as we know A and B can be two independent events if:
P(A∩B)=P(A)P(B)………………………………. (3)
And also, we know the relation among P(A),P(B),P(A∩B) and P(A∪B)is given :
P(A∪B)=P(A)+P(B)−P(A∩B)…………………. (4)
Now, we can use equations (1), (2), (3) to put the values of P(A),P(A∪B) and P(A∩B) to the equation (4) . So, we get the equation (4) as :
0.45=0.15+P(B)−P(A)P(B)
As, we know P(A)=0.15from the equation (1) , so, we can rewrite the above equation as:
0.45=0.15+P(B)−0.15P(B)
Or
0.45−0.15=P(B)−0.15P(B)0.30=P(B)−0.15P(B)
Now, we can take P(B) as common from both the terms of the right hand side of the above equation. So, we get 0.30=P(B)(1−0.15)
Or
0.30=P(B)×0.85
On dividing the above equation by 0.85, we get:
0.850.30=P(B)×0.850.85
Or P(B)=0.850.30
On multiplying the denominator and numerator by 100, we get:
P(B)=0.850.30×100100=8530P(B)=176
Hence, we get P(B)=176 . So, option (b) is the correct answer of the problem.
Note: One may use Venn diagram for the relation P(A) and P(B) as:
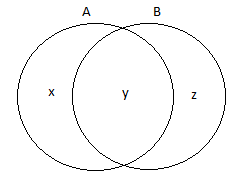
x+y=P(A)y+z=P(B)y=P(A∩B)x+y+z=P(A∪B)
Writing P(A∩B)=P(A)P(B) is the key point of the problem as A and B are independent events i.e. events A or B are not depending on each other.
