Question

If equations $ax^2 + (p+2)x + 10q = 0$ and $x^2+4x+5=0$ have a common root where a, p, q ∈N and λ = (a+p+q) has the least value then:

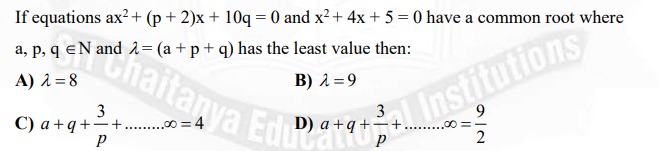
• A. λ = 8
• B. λ = 9
• C. $a+q+\frac{3}{p}+........_{\infty}=4$
• D. $a+q+\frac{3}{p}+........_{\infty}=\frac{9}{2}$

Answer 1

Answer: (B), (C)

λ = 9, $a+q+\frac{3}{p}+........_{\infty}=4$

Answer 2

The roots of the second equation $x^2+4x+5=0$ are given by the quadratic formula $x = \frac{-4 \pm \sqrt{4^2 - 4(1)(5)}}{2(1)} = \frac{-4 \pm \sqrt{16-20}}{2} = \frac{-4 \pm \sqrt{-4}}{2} = \frac{-4 \pm 2i}{2} = -2 \pm i$.
The roots are $x_1 = -2+i$ and $x_2 = -2-i$.

The first equation is $ax^2 + (p+2)x + 10q = 0$. The coefficients $a, p+2, 10q$ are real numbers since $a, p, q \in \mathbb{N}$ (natural numbers are positive integers).
If a polynomial equation with real coefficients has a complex root, then its conjugate must also be a root.
Since the two equations have a common root, and the roots of the second equation are complex conjugates, both roots of the second equation must be roots of the first equation.
This implies that the two quadratic equations have the same set of roots.
Therefore, the coefficients of the two equations must be proportional.
$\frac{a}{1} = \frac{p+2}{4} = \frac{10q}{5}$
Let the common ratio be $k$.
$a = k$
$p+2 = 4k \implies p = 4k-2$
$10q = 5k \implies q = \frac{5k}{10} = \frac{k}{2}$

We are given that $a, p, q \in \mathbb{N}$.
$a = k \in \mathbb{N}$
$p = 4k-2 \in \mathbb{N}$
$q = \frac{k}{2} \in \mathbb{N}$

For $q = k/2$ to be a natural number, $k$ must be an even natural number. Let $k = 2m$ for some $m \in \mathbb{N}$.
Then $a = 2m$.
$q = \frac{2m}{2} = m$.
$p = 4(2m) - 2 = 8m - 2$.

For $a \in \mathbb{N}$, $2m \in \mathbb{N}$, which is true for $m \in \mathbb{N}$.
For $q \in \mathbb{N}$, $m \in \mathbb{N}$.
For $p \in \mathbb{N}$, $8m - 2 \in \mathbb{N}$. Since $m \in \mathbb{N}$, the smallest value of $m$ is 1. If $m=1$, $p = 8(1)-2 = 6 \in \mathbb{N}$. If $m \ge 1$, $8m \ge 8$, so $8m-2 \ge 6$, which is a natural number.
So, $m$ can be any natural number ($m \in \{1, 2, 3, ...\}$).

We are given $\lambda = a+p+q$. We want to find the least value of $\lambda$.
Substitute the expressions in terms of $m$:
$\lambda = (2m) + (8m - 2) + (m) = 11m - 2$.
Since $m \in \mathbb{N}$, the smallest value of $m$ is 1.
The least value of $\lambda$ occurs when $m=1$.
Least $\lambda = 11(1) - 2 = 9$.
This occurs when $m=1$, which gives $k=2m=2$.
$a = 2m = 2$.
$p = 8m - 2 = 8(1) - 2 = 6$.
$q = m = 1$.
Check if $a, p, q \in \mathbb{N}$: $a=2 \in \mathbb{N}$, $p=6 \in \mathbb{N}$, $q=1 \in \mathbb{N}$. These values are valid.

Now we check the given options for these values $a=2, p=6, q=1$.
A) $\lambda = 8$. This is incorrect, the least value of $\lambda$ is 9.
B) $\lambda = 9$. This is correct, the least value of $\lambda$ is 9.

C) $a+q+\frac{3}{p}+........_{\infty}=4$
D) $a+q+\frac{3}{p}+........_{\infty}=\frac{9}{2}$
The series is $a+q+\frac{3}{p}+........_{\infty}$. Let's assume this is an infinite geometric series.
The first three terms are $a$, $q$, $\frac{3}{p}$.
If it is a GP, the common ratio $r$ must satisfy $r = q/a$ and $r = (3/p)/q$.
So, $\frac{q}{a} = \frac{3/p}{q} \implies q^2 = a \cdot \frac{3}{p} \implies pq^2 = 3a$.
Let's check this condition with $a=2, p=6, q=1$.
$pq^2 = 6(1)^2 = 6$.
$3a = 3(2) = 6$.
The condition $pq^2 = 3a$ is satisfied, which means the terms $a, q, \frac{3}{p}$ can be the first three terms of a geometric progression.
The first term of the GP is $A = a = 2$.
The common ratio is $r = q/a = 1/2$.
The third term is $Ar^2 = 2 (1/2)^2 = 2 (1/4) = 1/2$.
The given third term is $\frac{3}{p} = \frac{3}{6} = \frac{1}{2}$. This matches.
The infinite series is a geometric series with first term $A=2$ and common ratio $r=1/2$.
Since $|r| = 1/2 < 1$, the series converges.
The sum of the infinite geometric series is $S = \frac{A}{1-r} = \frac{a}{1-q/a} = \frac{2}{1-1/2} = \frac{2}{1/2} = 4$.

So, the value of the series $a+q+\frac{3}{p}+........_{\infty}$ is 4 for $a=2, p=6, q=1$.
C) $a+q+\frac{3}{p}+........_{\infty}=4$. This is correct.
D) $a+q+\frac{3}{p}+........_{\infty}=\frac{9}{2}$. This is incorrect.

Thus, options B and C are correct.