Question

If equations $ax^2 + (p+2)x + 10q = 0$ and $x^2 + 4x + 5 = 0$ have a common root

a, p, q ∈ N and λ = (a + p + q) has the least value then:

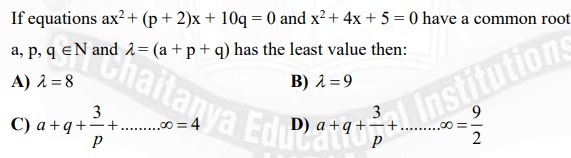
• A. λ = 8
• B. λ = 9
• C. $a + q + \frac{3}{p} + ........\infty = 4$
• D. $a + q + \frac{3}{p} + ........\infty = \frac{9}{2}$

Answer 1

Answer: (B), (C)

B, C

Answer 2

The two given quadratic equations are:

1. $ax^2 + (p+2)x + 10q = 0$
2. $x^2 + 4x + 5 = 0$

We are given that $a, p, q \in \mathbb{N}$ (natural numbers, i.e., positive integers). The discriminant of the second equation $x^2 + 4x + 5 = 0$ is $\Delta = 4^2 - 4(1)(5) = 16 - 20 = -4$. Since the discriminant is negative, the roots of the second equation are complex. The roots are $x = \frac{-4 \pm \sqrt{-4}}{2} = \frac{-4 \pm 2i}{2} = -2 \pm i$. The coefficients of the second equation are real (1, 4, 5). The coefficients of the first equation are $a$, $p+2$, and $10q$. Since $a, p, q \in \mathbb{N}$, these coefficients are integers and thus real.

If two quadratic equations with real coefficients have a common complex root, then the complex conjugate of that root must also be a root of both equations. This means both roots of the second equation must be roots of the first equation. Therefore, the two quadratic equations must have the same roots. This implies that the equations are proportional. So, the ratio of corresponding coefficients must be equal: $\frac{a}{1} = \frac{p+2}{4} = \frac{10q}{5}$ Let this common ratio be $k$. $a = k$ $p+2 = 4k$ $10q = 5k \implies 2q = k$

From $k = 2q$, we can express $a$ and $p$ in terms of $q$: $a = 2q$ $p+2 = 4(2q) = 8q \implies p = 8q - 2$

We are given that $a, p, q \in \mathbb{N}$. For $q \in \mathbb{N}$, $q \ge 1$. $a = 2q$. Since $q \ge 1$, $a$ is an even positive integer, so $a \in \mathbb{N}$. $p = 8q - 2$. Since $q \ge 1$, $8q \ge 8$, so $8q - 2 \ge 6$. Thus $p$ is a positive integer, so $p \in \mathbb{N}$.

We want to find the least value of $\lambda = a + p + q$. Substitute the expressions for $a$ and $p$ in terms of $q$: $\lambda = (2q) + (8q - 2) + q = 11q - 2$. To minimize $\lambda$, we must minimize $q$, since $q \in \mathbb{N}$. The smallest value $q$ can take is 1. When $q=1$: $a = 2(1) = 2$. This is in $\mathbb{N}$. $p = 8(1) - 2 = 6$. This is in $\mathbb{N}$. $q = 1$. This is in $\mathbb{N}$. These values satisfy the conditions $a, p, q \in \mathbb{N}$. The minimum value of $\lambda$ is obtained when $q=1$: $\lambda_{min} = 11(1) - 2 = 9$.

So, the least value of $\lambda = a+p+q$ is 9, occurring when $a=2, p=6, q=1$. Now we check the given options based on these values.

A) $\lambda = 8$: This is false, as $\lambda_{min} = 9$. B) $\lambda = 9$: This is true, as $\lambda_{min} = 9$.

C) $a + q + \frac{3}{p} + ........\infty = 4$: Let's evaluate the series with $a=2, q=1, p=6$. The series is $2 + 1 + \frac{3}{6} + \dots = 2 + 1 + \frac{1}{2} + \dots$. This appears to be an infinite geometric series. Let's check the ratio of consecutive terms: Ratio of the second term to the first term: $1/2$. Ratio of the third term to the second term: $(1/2)/1 = 1/2$. The terms $a, q, 3/p, \dots$ form a geometric progression with first term $A = a = 2$ and common ratio $R = 1/2$. Since $|R| = 1/2 < 1$, the series converges. The sum of an infinite geometric series is $S = \frac{A}{1-R}$. $S = \frac{2}{1 - 1/2} = \frac{2}{1/2} = 4$. So, $a + q + \frac{3}{p} + ........\infty = 4$ is true for $a=2, q=1, p=6$.

D) $a + q + \frac{3}{p} + ........\infty = \frac{9}{2}$: This is false, as the sum is 4.

Based on the condition that $\lambda = a+p+q$ has the least value (which is 9, occurring at $a=2, p=6, q=1$), options B and C are true. The question asks to return all correct options.