Question

If equation of sound wave is $y = 0.0015\sin (62.4x + 316t)$ , then its wavelength will be

(A) 2 unit

(B) 0.3unit

(C) 0.1unit

(D) 0.2 unit

Answer 1

The given equation takes the exact form of the progressive wave equation$y = A\sin (\omega t - kx)$. So, on comparing both the wave functions, find out the value of the propagation constant k. k is related to the wavelength by $k = \dfrac{{2\pi }}{\lambda }$ . Now on substituting the values calculate the wavelength of the wave.

Complete step-by-step answer
A mathematical description of the disturbance created by a wave is called a wave function.

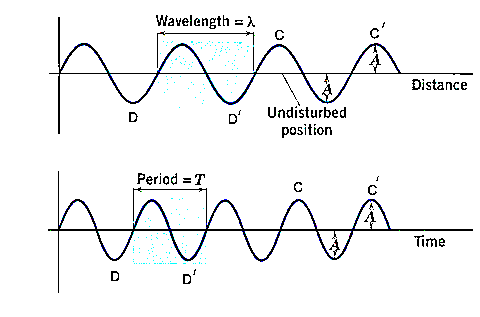
We know that, a progressive wave function is given by,
$y = A\sin (\omega t - kx)$

Where,
Y is the displacement; A is the amplitude; $\omega$is the angular frequency; x is the position; k is the propagation constant and t is the time.
$y = 0.0015\sin (62.4x + 316t)$

The given equation is similar to this wave function and therefore has corresponding values. On comparing with the progressive wave function we find out the value of the propagation constant also known as angular wave number.
$k = 62.8$

The number of wavelengths in the distance$2\pi$is called the wave number which is given by,
$k = \dfrac{{2\pi }}{\lambda }$

Substitute the value of the angular wave number.

$\lambda = \dfrac{{2 \times 3.14}}{{62.8}}$

$\lambda = 0.1unit$

Hence, the wavelength of the wave is 0.1 units and the correct option is C.

Note: If during the propagation of a progressive wave, the particles of the medium perform SHM about their mean position then the wave is known as a harmonic progressive wave. Various forms of progressive wave function.

$y = A\sin 2\pi \left( {\dfrac{t}{T} - \dfrac{x}{\lambda }} \right)$

$y = A\sin \dfrac{{2\pi }}{T}\left( {t - \dfrac{{xT}}{\lambda }} \right)$

$y = A\sin \dfrac{{2\pi }}{\lambda }\left( {vt - x} \right)$

$y = A\sin \omega \left( {t - \dfrac{x}{v}} \right)$

We can also write it in exponential form

$y = A\dfrac{{{e^{i\omega \left( {t - \dfrac{x}{v}} \right)}} - {e^{ - i\omega \left( {t - \dfrac{x}{v}} \right)}}}}{{2i}}$