Question
Question: If eqn $x^4-x^3+3x^2-7x+8=0$ has nots $\alpha, \beta, \gamma, \delta$ then find value of $(2-\alpha)...
If eqn x4−x3+3x2−7x+8=0 has nots α,β,γ,δ then find value of (2−α).(2−β).(2−γ).(2−δ)
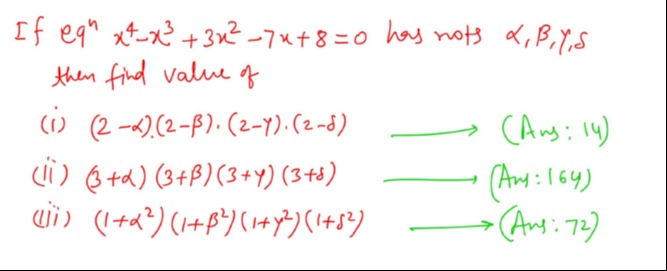
Answer
14
Explanation
Solution
Let the given polynomial be P(x)=x4−x3+3x2−7x+8. Since α,β,γ,δ are the roots of the equation P(x)=0, we can write the polynomial in factored form as: P(x)=(x−α)(x−β)(x−γ)(x−δ) The expression (2−α).(2−β).(2−γ).(2−δ) is equivalent to P(2). Substituting x=2 into P(x): P(2)=(2)4−(2)3+3(2)2−7(2)+8 P(2)=16−8+3(4)−14+8 P(2)=16−8+12−14+8 P(2)=14
