Question
Question: If enthalpy of hydrogenation of \({{\text{C}}_{\text{6}}}{{\text{H}}_{\text{6}}}\left( {\text{l}} \r...
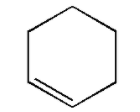
If enthalpy of hydrogenation of C6H6(l) into C6H12(l) is −205 kJ and resonance energy of C6H6(l) is −152 kJ/mol then enthalpy of hydrogenation of the given figure is:
[Assume: ΔHvap of C6H6(l), C6H8(l), C6H12(l) are all equal]
A. +535.5 kJ/mol
B. −238 kJ/mol
C. −357 kJ/mol
D. −119 kJ/mol
Solution
We know that benzene (C6H6(l)) contains three double bonds. To break these three bonds and convert benzene (C6H6(l)) to cyclohexane (C6H12(l)) three molecules of hydrogen (H2) will be required. To calculate the enthalpy of hydrogenation of the given compound we must add resonance energy to the total enthalpy of the reaction.
Complete step by step solution:
We are given that the enthalpy of hydrogenation of benzene (C6H6(l)) is −205 kJ and the resonance energy of benzene as −152 kJ/mol.
To calculate the actual enthalpy of hydrogenation of benzene if there is no resonance we add the enthalpy of hydrogenation and the resonance energy. Thus,
ΔHcyclohexene=ΔHbenzene+Resonance energy
Where ΔHcyclohexene is the enthalpy of hydrogenation of cyclohexene,
ΔHbenzene is the enthalpy of hydrogenation of benzene.
Substitute −205 kJ for the enthalpy of hydrogenation of benzene, −152 kJ/mol for the resonance energy of benzene and solve for the enthalpy of hydrogenation of cyclohexene. Thus,
ΔHcyclohexene=(−205 kJ/mol)+(−152 kJ/mol)
ΔHcyclohexene=−357 kJ/mol
Thus, the actual enthalpy of hydrogenation of benzene is −357 kJ/mol.
The hydrogenation reaction of benzene is as follows:
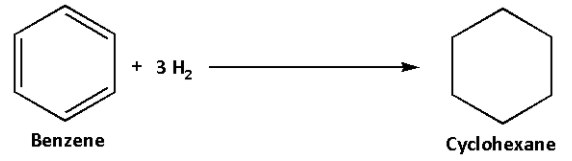
In this reaction, three bonds break and three hydrogen molecules are required.
In the given figure i.e. cyclohexene there is only one double bond. Thus, only one molecule of hydrogen will be required for the breaking of the bond.
Thus, enthalpy of hydrogenation of cyclohexene will be,
ΔHcyclohexene=3ΔHbenzene
Where ΔHcyclohexene is the enthalpy of hydrogenation of cyclohexene,
ΔHbenzene is the enthalpy of hydrogenation of benzene.
Substitute −357 kJ/mol for the enthalpy of hydrogenation of benzene. Thus,
ΔHcyclohexene=3−357 kJ/mol
ΔHcyclohexene=−119 kJ/mol
Thus, the enthalpy of hydrogenation of the given figure is −119 kJ/mol.
**Thus, the correct option is (D) −119 kJ/mol.
Note: **
Do not forget to consider the signs of enthalpy of hydrogenation and the resonance energy in the calculation. To break one pi-bond one molecule of hydrogen is required.
