Question

If each of the vertices of a triangle has integral co – ordinates then the triangle may be
(a) Right angled
(b) Equilateral
(c) Isosceles
(d) None of these

Answer 1

Hint : To solve this question we will consider all the points (a), (b), (c) and (d) separately. We will assume integral co – ordinates for all the three given types of triangles and then if any contradiction is coming or not. If no contraction is coming then there is a possibility of that triangle to have integral co – ordinates.

Complete step-by-step answer :
Given that each of the vertices of the triangle has integral co – ordinates.
We will check all options one by one and see which of the options is possible and which is not.
Consider option (a) Right angle triangle.
If we take (0, 0) as one of the axis then by taking integral co – ordinates on x – axis and y – axis we can form right angled triangle as,
Let vertices be (0, 0), (3, 0) and (0, 5) then right angle triangle would be,

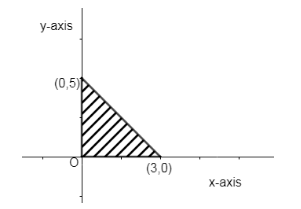
Hence option (a) is possible.
Now consider option (b) Equilateral triangle.
Let $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ are co – ordinates of the three vertices.
Then area = $\dfrac{1}{2}\left| \begin{matrix} 1 & 1 & 1 \\\ {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\\ {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\\ \end{matrix} \right|$
If all the co – ordinates are integers then the value of the above determinant is rational number. – (1)
Now if the above triangle is an equilateral triangle then area of triangle = $\dfrac{\sqrt{3}}{4}\times {{\left( side \right)}^{2}}$.
For integer co – ordinates ${{\left( side \right)}^{2}}$ = positive integers.
But as $\dfrac{\sqrt{3}}{4}$ is irrational
So, $\dfrac{\sqrt{3}}{4}\times {{\left( side \right)}^{2}}$ would be irrational. – (2)
(1) and (2) are contracting statements.
So, (b) is an incorrect option.
(c) Consider option (c).
Again we take (0, 0) and (4, 0) are two points and any third point on x = 2 will form an isosceles triangle with (0, 0), (4, 0) and (2, 6).
Hence the point (0, 0), (4, 0) and (2, 6) will form an isosceles triangle.
So, option (c) is also possible.
Figure is as,

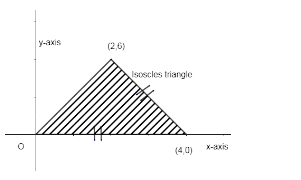
So, the correct answer is “Option And C”.

Note : The possibility of error in this question can be at the point where we have to consider the equilateral triangle. Do not go for taking and then prove the result. We generally have to show that equilateral triangle is not a possibility and not with any triangle of any measure. This way the solution would be exactly correct and free from errors.