Solveeit Logo
Login

Question

Question: If E and F are independent events such that \(0 < P ( E ) < 1\) and \(0 < P ( F ) < 1\) then...

If E and F are independent events such that 0<P(E)<10 < P ( E ) < 1 and 0<P(F)<10 < P ( F ) < 1 then

A

E and FcF ^ { c }(the complement of the event F) are independent

B

EcE ^ { c }and FcF ^ { c }are independent

C

P(EF)+P(EcFc)=1P \left( \frac { E } { F } \right) + P \left( \frac { E ^ { c } } { F ^ { c } } \right) = 1

D

All of the above

Answer

All of the above

Explanation

Solution

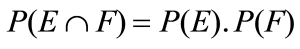
Now, P(E∩Fc)=P(E)−P(E∩F)=P(E)[1−P(F)]=P(E)⋅P(Fc)P \left( E \cap F ^ { c } \right) = P ( E ) - P ( E \cap F ) = P ( E ) [ 1 - P ( F ) ] = P ( E ) \cdot P \left( F ^ { c } \right)

and P(Ec∩Fc)=1−P(E∪F)=1−[P(E)+P(F)−P(E∩F)P \left( E ^ { c } \cap F ^ { c } \right) = 1 - P ( E \cup F ) = 1 - [ P ( E ) + P ( F ) - P ( E \cap F )

=[1−P(E)][1−P(F)]=P(Ec)P(Fc)= [ 1 - P ( E ) ] [ 1 - P ( F ) ] = P \left( E ^ { c } \right) P \left( F ^ { c } \right)

Also P(E/F)=P(E)P ( E / F ) = P ( E ) and P(Ec/Fc)=P(Ec)P \left( E ^ { c } / F ^ { c } \right) = P \left( E ^ { c } \right)

⇒P(E/F)+P(Ec/Fc)=1\Rightarrow P ( E / F ) + P \left( E ^ { c } / F ^ { c } \right) = 1