Question

If ${e_1}$ and ${e_2}$ are the eccentricities of a hyperbola and its conjugate then ${e_1}^2 + {e_2}^2$ will be
A. 1
B. ${e_1}^2{e_2}^2$
C. 0
D.$\dfrac{1}{{{e_1}^2}} + \dfrac{1}{{{e_2}^2}}$

Answer 1

Here we assume a general hyperbola and write its conjugate. Use the formula for eccentricity of a hyperbola and write both the eccentricities. Square each eccentricity and add to obtain the value of sum.

• General equation of a hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$, where the center is the origin and vertices are $( \pm a,0)$ and co vertices are $(0, \pm b)$. The transverse axis is x-axis and conjugate axis is y-axis
• Eccentricity of a hyperbola measures the degree of opening of branches of hyperbola and is given by the formula $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$.
• Conjugate of a hyperbola is a hyperbola where the transversal axis becomes the conjugate axis and the conjugate axis becomes the transverse axis.

Complete step-by-step answer:
Let us assume a hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ … (1)

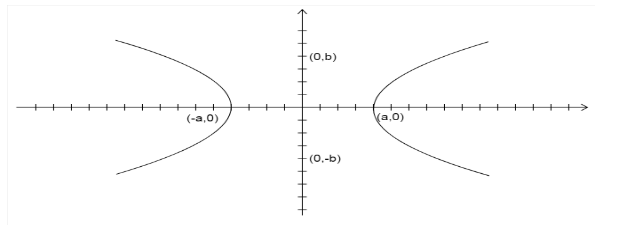
Where the center is the origin and vertices are $( \pm a,0)$ and co vertices are $(0, \pm b)$. The transverse axis is the x-axis and the conjugate axis is y-axis.
The formula of eccentricity of a hyperbola is $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
Then eccentricity of hyperbola in equation (1) is
$\Rightarrow {e_1} = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
Square both sides of the equation
$\Rightarrow {e_1}^2 = {\left( {\dfrac{{\sqrt {{a^2} + {b^2}} }}{a}} \right)^2}$
Cancel square root by square power.
$\Rightarrow {e_1}^2 = \dfrac{{{a^2} + {b^2}}}{{{a^2}}}$ … (2)
Then the conjugate of the hyperbola in equation (1) is $\dfrac{{{y^2}}}{{{b^2}}} - \dfrac{{{x^2}}}{{{a^2}}} = 1$ … (3)

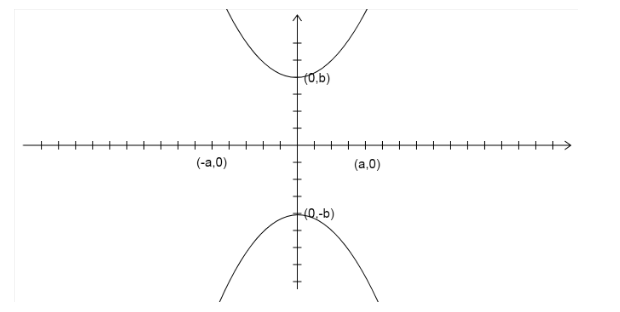
Where the center is the origin and vertices are $(0, \pm b)$ and co vertices are $( \pm a,0)$. The transverse axis is the y-axis and the conjugate axis is x-axis.
The formula of eccentricity of a hyperbola is $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
Then eccentricity of hyperbola in equation (3) is
$\Rightarrow {e_2} = \dfrac{{\sqrt {{a^2} + {b^2}} }}{b}$
Square both sides of the equation
$\Rightarrow {e_2}^2 = {\left( {\dfrac{{\sqrt {{a^2} + {b^2}} }}{b}} \right)^2}$
Cancel square root by square power.
$\Rightarrow {e_2}^2 = \dfrac{{{a^2} + {b^2}}}{{{b^2}}}$ … (4)
Add equations (2) and (4)
$\Rightarrow {e_1}^2 + {e_2}^2 = \dfrac{{{a^2} + {b^2}}}{{{a^2}}} + \dfrac{{{a^2} + {b^2}}}{{{b^2}}}$
Take ${a^2} + {b^2}$common from the numerators of both fractions in RHS
$\Rightarrow {e_1}^2 + {e_2}^2 = \left( {{a^2} + {b^2}} \right)\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)$
Take LCM of the two fractions in the bracket in RHS
$\Rightarrow {e_1}^2 + {e_2}^2 = \left( {{a^2} + {b^2}} \right)\left( {\dfrac{{{b^2} + {a^2}}}{{{a^2}{b^2}}}} \right)$
Break the denominator by multiplication
$\Rightarrow {e_1}^2 + {e_2}^2 = \left( {\dfrac{{{a^2} + {b^2}}}{{{a^2}}}} \right)\left( {\dfrac{{{b^2} + {a^2}}}{{{b^2}}}} \right)$
Substitute the value of ${e_1}^2 = \dfrac{{{a^2} + {b^2}}}{{{a^2}}}$from equation (2) and ${e_2}^2 = \dfrac{{{a^2} + {b^2}}}{{{b^2}}}$from equation (4) in RHS of the equation.
$\Rightarrow {e_1}^2 + {e_2}^2 = {e_1}^2{e_2}^2$

So, the correct option is B.

Note: Students might get confused as many books write the conjugate of the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ as $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = - 1$ which is same as the hyperbola $\dfrac{{{y^2}}}{{{b^2}}} - \dfrac{{{x^2}}}{{{a^2}}} = 1$ if we multiply -1 throughout. Also, when solving the addition of terms it is easier if we take out common terms first, else the calculations become complex.