Question

If ${e_1}$ and ${e_2}$ are respectively the eccentricities of the ellipse $\dfrac{{{x^2}}}{{18}} + \dfrac{{{y^2}}}{4} = 1$ and the hyperbola $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{4} = 1$ , then the relation between ${e_1}$ and ${e_2}$ is
(A) $3{e_1}^2 + {e_2}^2 = 2$
(B) ${e_1}^2 + 2{e_2}^2 = 3$
(C) $2{e_1}^2 + {e_2}^2 = 3$
(D) ${e_1}^2 + 3{e_2}^2 = 2$

Answer 1

Hint : We compare $\dfrac{{{x^2}}}{{18}} + \dfrac{{{y^2}}}{4} = 1$ with the equation of an ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ to get the values of $a$ and $b$ and compute its eccentricity ${e_1}$ using ${e_1} = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$ . Similarly, we compare $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{4} = 1$ with the equation of hyperbola and find ${e_2}$ using ${e_2} = \sqrt {1 + \dfrac{{{b^2}}}{{{a^2}}}}$ . Then, we need to substitute ${e_1}$ and ${e_2}$ in the LHS of each option to determine the correct relation.

Complete step-by-step answer :
We are given two equations: $\dfrac{{{x^2}}}{{18}} + \dfrac{{{y^2}}}{4} = 1$ and $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{4} = 1$
Here $\dfrac{{{x^2}}}{{18}} + \dfrac{{{y^2}}}{4} = 1$ is the equation of an ellipse and $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{4} = 1$ is the equation of a hyperbola
The eccentricities of these geometrical figures are denoted by the notation ${e_1}$ and ${e_2}$ respectively in the question.
We are asked to determine the relation between ${e_1}$ and ${e_2}$ .
Let us number the given equations as follows:
$\dfrac{{{x^2}}}{{18}} + \dfrac{{{y^2}}}{4} = 1......(1)$
$\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{4} = 1.....(2)$
The standard form of the equation of an ellipse with center at the origin $(0,0)$ and major axis parallel to the X-axis is given by $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
Where $a,b$ are two real numbers and $a > b$

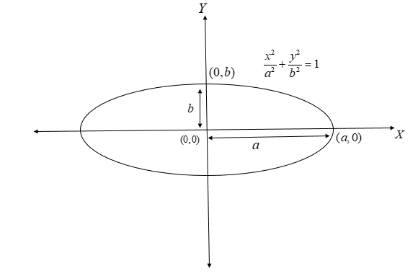
The eccentricity of this ellipse is given by the formula ${e_1} = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$
Therefore, from equation (1), we have ${a^2} = 18$ and ${b^2} = 4$
This implies that we get ${e_1} = \sqrt {1 - \dfrac{4}{{18}}} = \sqrt {\dfrac{{14}}{{18}}}$
For a hyperbola centered at the origin $(0,0)$ with transverse axis on the X-axis, the standard form of its equation is given by$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$

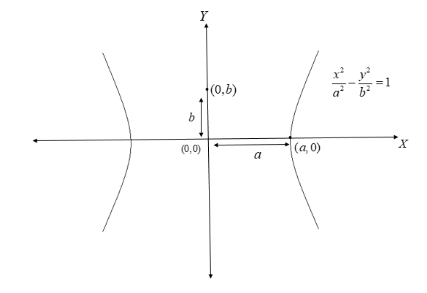
The eccentricity of this hyperbola is given by ${e_2} = \sqrt {1 + \dfrac{{{b^2}}}{{{a^2}}}}$
Therefore, from equation (2), we have ${a^2} = 9$ and ${b^2} = 4$ .
This implies that we get ${e_2} = \sqrt {1 + \dfrac{4}{9}} = \sqrt {\dfrac{{13}}{9}}$
Thus, we get ${e_1}^2 = \dfrac{{14}}{{18}}$ and ${e_2}^2 = \dfrac{{13}}{9}$
On multiplying ${e_1}^2$ by 2, we get $2{e_1}^2 = 2 \times \dfrac{{14}}{{18}} = \dfrac{{14}}{9}$ .
Similarly, $3{e_1}^2 = \dfrac{{14}}{6}$ , $2{e_2}^2 = \dfrac{{26}}{9}$ , and $3{e_2}^2 = \dfrac{{13}}{3}$
Let’s check each option:
A) $3{e_1}^2 + {e_2}^2 = 2$ $\Rightarrow 3{e_1}^2 + {e_2}^2 = \dfrac{{14}}{6} + \dfrac{{13}}{9} = \dfrac{{42 + 26}}{{18}} = \dfrac{{68}}{{18}} \ne 2$
(B) ${e_1}^2 + 2{e_2}^2 = 3$ $\Rightarrow {e_1}^2 + 2{e_2}^2 = \dfrac{{14}}{{18}} + \dfrac{{26}}{9} = \dfrac{{14 + 52}}{{18}} = \dfrac{{66}}{{18}} \ne 3$
(C) $2{e_1}^2 + {e_2}^2 = 3$ $\Rightarrow 2{e_1}^2 + {e_2}^2 = \dfrac{{14}}{9} + \dfrac{{13}}{9} = \dfrac{{14 + 13}}{9} = \dfrac{{27}}{9} = 3$
(D) ${e_1}^2 + 3{e_2}^2 = 2$ $\Rightarrow {e_1}^2 + 3{e_2}^2 = \dfrac{{14}}{{18}} + \dfrac{{13}}{3} = \dfrac{{14 + 78}}{{18}} = \dfrac{{92}}{{18}} \ne 2$
Hence $2{e_1}^2 + {e_2}^2 = 3$ is the correct answer.

So, the correct answer is “Option C”.

Note : 1) There are two axes in an ellipse: the major axis and the minor axis. They are nothing but the longest and the shortest diameters respectively of the ellipse.
2) The transverse axis of a hyperbola is the segment passing through its center with the vertices of hyperbola as its endpoints. Here, by vertices, we mean the points at which the curves of the hyperbola intersect the coordinate axis.