Question
Question: If domain of f(x) is (-∞, 0], then domain of f (6\{x\}$^2$-5\{x\}+1) is (where \{\} represents fract...
If domain of f(x) is (-∞, 0], then domain of f (6{x}2-5{x}+1) is (where {} represents fractional part function)
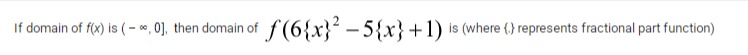
⋃n∈Z[n+31,n+21]
Solution
The problem asks for the domain of the composite function f(g(x)), where f(x) has a domain of (−∞,0] and g(x)=6{x}2−5{x}+1. Here, {⋅} represents the fractional part function.
For f(g(x)) to be defined, the argument of f must be within its domain. Given that the domain of f(x) is (−∞,0], we must have g(x)≤0. So, we need to solve the inequality: 6{x}2−5{x}+1≤0
Let y={x}. We know that the range of the fractional part function is 0≤{x}<1. Substitute y into the inequality: 6y2−5y+1≤0
To solve this quadratic inequality, we first find the roots of the corresponding quadratic equation 6y2−5y+1=0. We can factorize the quadratic expression: 6y2−3y−2y+1=0 3y(2y−1)−1(2y−1)=0 (3y−1)(2y−1)=0
The roots are y=31 and y=21.
Since the coefficient of y2 (which is 6) is positive, the parabola 6y2−5y+1 opens upwards. Therefore, the quadratic expression is less than or equal to zero between its roots. So, the inequality 6y2−5y+1≤0 holds when: 31≤y≤21
Now, substitute back y={x}: 31≤{x}≤21
We need to find the values of x for which its fractional part lies in the interval [31,21]. The fractional part of x, denoted by {x}, is defined as {x}=x−⌊x⌋, where ⌊x⌋ is the greatest integer less than or equal to x. Let n=⌊x⌋, where n is an integer (n∈Z). Then the inequality becomes: 31≤x−n≤21
To find x, we add n to all parts of the inequality: n+31≤x≤n+21
Since this condition must hold for any integer n, the domain of the function f(6{x}2−5{x}+1) is the union of all such intervals for all integers n.
Domain =⋃n∈Z[n+31,n+21]
The domain consists of an infinite number of disjoint closed intervals. For example, for n=0, x∈[31,21]; for n=1, x∈[34,23]; for n=−1, x∈[−32,−21], and so on.
