Question

If $\dfrac{{\tan 3\theta }}{{\tan \theta }} = 4$ , then $\dfrac{{\sin 3\theta }}{{\sin \theta }}$ equals:
(A) $\dfrac{8}{3}$
(B) $\dfrac{4}{5}$
(C) $\dfrac{3}{4}$
(D) None of these

Answer 1

According to the question, use the formula $\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}$ and simplify to get the value of $\tan \theta$ and calculate the value in terms of sin to find the required answer. Then again use the formula of $\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta$ to find the value of $\dfrac{{\sin 3\theta }}{{\sin \theta }}$.

Formula used:
Here, we use the trigonometric formulas that is $\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}$ and $\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta$.

Complete step by step solution:
As it is given, $\dfrac{{\tan 3\theta }}{{\tan \theta }} = 4$
Take $\tan \theta$ on the right hand side in multiply.
So we get, $\tan 3\theta = 4\tan \theta$
Here, we will use the formula of $\tan 3\theta = \dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}$
On substituting we get,
$\dfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }} = 4\tan \theta$
Taking $\tan \theta$ common in numerator from right hand side,
$\dfrac{{\tan \theta \left( {3 - {{\tan }^2}\theta } \right)}}{{1 - 3{{\tan }^2}\theta }} = 4\tan \theta$
Cancelling $\tan \theta$ from both right hand side and left hand side,
So we get,
$\dfrac{{3 - {{\tan }^2}\theta }}{{1 - 3{{\tan }^2}\theta }} = 4$
Taking denominator of left hand side to the right hand side,
$3 - {\tan ^2}\theta = 4(1 - 3{\tan ^2}\theta )$
$3 - {\tan ^2}\theta = 4 - 12{\tan ^2}\theta$
After simplifying we get,
$- {\tan ^2}\theta + 12{\tan ^2}\theta = 4 - 3$
$11{\tan ^2}\theta = 1$
So, ${\tan ^2}\theta = \dfrac{1}{{11}}$
After taking square root on both side we get,
$\tan \theta = \sqrt {\dfrac{1}{{11}}}$
As we know $\sqrt 1 = 1$ and $\sqrt {11} = \sqrt {11}$
Substituting all the calculated values we get,
$\tan \theta = \dfrac{1}{{\sqrt {11} }}$
As we know $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$
So, we will draw a right angled triangle $\Delta ABC$ having angle $\theta$ , base $= \sqrt {11}$ and perpendicular = 1 as shown in figure.

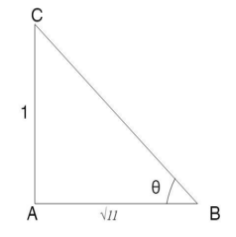
As of now we will calculate Hypotenuse by using the Pythagoras theorem that is ${H^2} = {P^2} + {B^2}$
So, we will substitute all the values of P and B to get the value of H .
In right angled triangle $\Delta ABC$
${H^2} = {1^2} + {\left( {\sqrt {11} } \right)^2}$
After calculating squares we get,
${H^2} = 1 + 11$
${H^2} = 12$
After taking square root on both side we get,
$H = \sqrt {12} = 2\sqrt 3$
So, now we will calculate $\sin \theta = \dfrac{P}{H}$
Putting P = 1 and $H = 2\sqrt 3$ we get,
$\sin \theta = \dfrac{1}{{2\sqrt 3 }}$
As, according to the question we have to calculate $\dfrac{{\sin 3\theta }}{{\sin \theta }}$
Here, we use the formula of $\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta$
After substituting we get,
$\Rightarrow \dfrac{{3\sin \theta - 4{{\sin }^3}\theta }}{{\sin \theta }}$
Taking $\sin \theta$ common from numerator and cancelling $\sin \theta$ from numerator and denominator we get,
$\Rightarrow 3 - 4{\sin ^2}\theta$
Putting the value of $\sin \theta = \dfrac{1}{{2\sqrt 3 }}$ in the above equation.
$\Rightarrow 3 - 4{\left( {\dfrac{1}{{2\sqrt 3 }}} \right)^2}$
On simplifying we get,
$\Rightarrow 3 - \dfrac{1}{3}$
By taking L.C.M we get,
$\Rightarrow \dfrac{8}{3}$

So, option (A) $\dfrac{8}{3}$ is correct.

Note:
To solve these types of questions, you must remember the trigonometric formulas and conversion of trigonometric values. For conversion you can simply use Pythagoras theorem to find the required value.