Question

If $\dfrac{1+4p}{4},\dfrac{1-p}{2},\dfrac{1-2p}{2}$ are the probabilities of three mutually exclusive events, then
$\left( a \right)\dfrac{1}{3}\le p\le \dfrac{1}{2}$
$\left( b \right)\dfrac{1}{3}\le p\le \dfrac{2}{3}$
$\left( c \right)\dfrac{1}{6}\le p\le \dfrac{1}{2}$
(d) None of these

Answer 1

Let us assume the given probabilities as probabilities of events A, B and C respectively. Consider the conditions: $0\le P\left( A \right)\le 1,0\le P\left( B \right)\le 1,0\le P\left( C \right)\le 1,0\le P\left( A \right)+P\left( B \right)+P\left( C \right)\le 1$ and find the range of p in all four cases. Then, finally, take the intersection of the sets of p obtained in the four conditions to get the answer.

Complete step-by-step solution:
Here, we have been provided with the probabilities of three mutually exclusive events. Let us assume these events as A, B and C. So, we have,
$P\left( A \right)=\dfrac{1+4p}{4}$
$P\left( B \right)=\dfrac{1-p}{2}$
$P\left( C \right)=\dfrac{1-2p}{2}$
Now, two or more events are said to be mutually exclusive if they cannot occur at the same time. For example, when a coin is tossed then the event of occurring head and tail cannot occur at the same time. Therefore, the tossing of a coin is an example of a mutually exclusive event. The condition for three events to be mutually exclusive is:
$P\left( A\cup B\cup C \right)=P\left( A \right)+P\left( B \right)+P\left( C \right)......\left( i \right)$
Now we know that the probability of any event lies in the interval [0, 1]. Therefore, $0\le P\left( A \right)\le 1,0\le P\left( B \right)\le 1,0\le P\left( C \right)\le 1,0\le P\left( A\cup B\cup C \right)\le 1.$ So, let us consider each condition one – by one.
$\left( 1 \right)0\le P\left( A \right)\le 1$
$\Rightarrow 0\le \dfrac{1+4p}{4}\le 1$
$\Rightarrow 0\le 1+4p\le 4$
$\Rightarrow -1\le 4p\le 3$
$\Rightarrow \dfrac{-1}{4}\le p\le \dfrac{3}{4}.....\left( ii \right)$
$\left( 2 \right)0\le P\left( B \right)\le 1$
$\Rightarrow 0\le \dfrac{1-p}{2}\le 1$
$\Rightarrow 0\le 1-p\le 2$
$\Rightarrow -1\le -p\le 1$
Multiplying all the terms with – 1 and reversing the inequality direction, we get,
$\Rightarrow -1\le p\le 1.....\left( iii \right)$
$\left( 3 \right)0\le P\left( C \right)\le 1$
$\Rightarrow 0\le \dfrac{1-2p}{2}\le 1$
$\Rightarrow 0\le 1-2p\le 2$
$\Rightarrow -1\le -2p\le 1$
$\Rightarrow \dfrac{-1}{2}\le -p\le \dfrac{1}{2}$
Multiplying all the terms with – 1 and reversing the inequality direction, we get,
$\Rightarrow \dfrac{-1}{2}\le p\le \dfrac{1}{2}.....\left( iv \right)$
$\left( 4 \right)0\le P\left( A\cup B\cup C \right)\le 1$
Substituting the value of $P\left( A\cup B\cup C \right)$ from equation (i), we get,
$\Rightarrow 0\le P\left( A \right)+P\left( B \right)+P\left( C \right)\le 1$
$\Rightarrow 0\le \dfrac{1+4p}{4}+\dfrac{1-p}{2}+\dfrac{1-2p}{2}\le 1$
$\Rightarrow 0\le \dfrac{1+4p+2-2p+2-4p}{4}\le 1$
$\Rightarrow 0\le \dfrac{5-2p}{4}\le 1$
$\Rightarrow 0\le 5-2p\le 4$
$\Rightarrow -5\le -2p\le -1$
$\Rightarrow \dfrac{-5}{2}\le -p\le \dfrac{-1}{2}$
Multiplying all the terms and reversing the inequality direction, we get,
$\Rightarrow \dfrac{1}{2}\le p\le \dfrac{5}{2}.....\left( v \right)$
To find the interval of values of p we must take the intersection of the sets of the values of p given in the equations (ii), (iii), (iv), and (v). So, let us draw a number line for this.

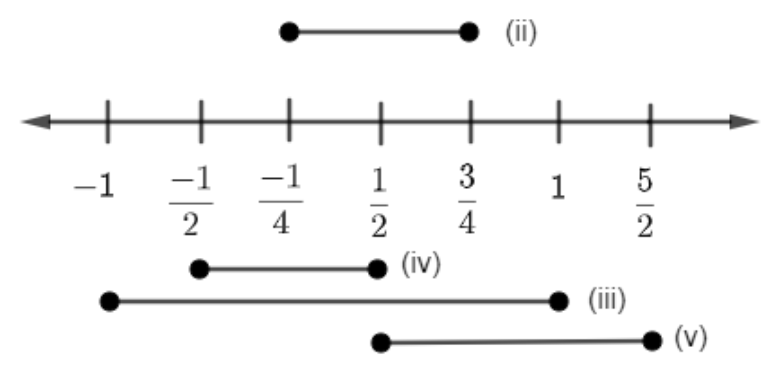
**Clearly, we can see that $p=\dfrac{1}{2}$ is the only common value.
Hence, option (d) is the right answer. **

Note: One must remember the definition of a mutually exclusive event and its condition to solve the above question. Always remember that while solving the inequalities when we multiply the terms with a negative number then the direction of inequality gets reversed. It is important for us to draw the sets on the number line so that we can easily visualize the intervals and do not get confused.