Solveeit Logo
Login

Question

Question: If $D_r = \begin{vmatrix} \frac{2}{2r-1} & 3 \\ 0 & \frac{1}{2r+1} \end{vmatrix}$ then $\sum_{r=1}^{...

If Dr=∣22r−13012r+1∣D_r = \begin{vmatrix} \frac{2}{2r-1} & 3 \\ 0 & \frac{1}{2r+1} \end{vmatrix} then ∑r=1nDr\sum_{r=1}^{n} D_r equals

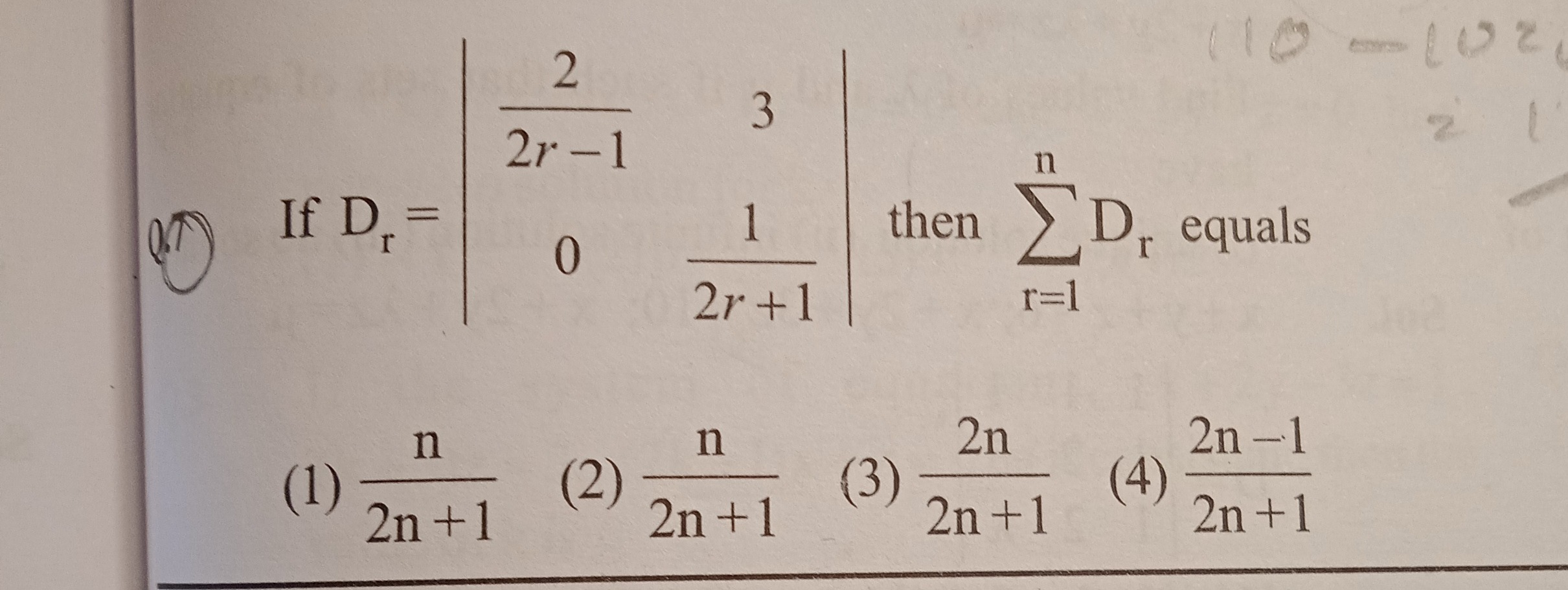
A

n2n+1\frac{n}{2n+1}

B

n2n+1\frac{n}{2n+1}

C

2n2n+1\frac{2n}{2n+1}

D

2n−12n+1\frac{2n-1}{2n+1}

Answer

2n2n+1\frac{2n}{2n+1}

Explanation

Solution

Given

Dr=∣22r−13012r+1∣,D_r = \begin{vmatrix} \frac{2}{2r-1} & 3 \\ 0 & \frac{1}{2r+1} \end{vmatrix},

its determinant is

Dr=2(2r−1)(2r+1).D_r = \frac{2}{(2r-1)(2r+1)}.

Step 1: Write the sum:

∑r=1nDr=∑r=1n2(2r−1)(2r+1).\sum_{r=1}^{n} D_r = \sum_{r=1}^{n} \frac{2}{(2r-1)(2r+1)}.

Step 2: Use partial fractions: Assume

2(2r−1)(2r+1)=A2r−1+B2r+1.\frac{2}{(2r-1)(2r+1)} = \frac{A}{2r-1} + \frac{B}{2r+1}.

Multiplying through by (2r−1)(2r+1)(2r-1)(2r+1):

2=A(2r+1)+B(2r−1).2 = A(2r+1) + B(2r-1).

Equate coefficients:

  • For rr: 2A+2B=0  ⟹  A=−B.2A + 2B = 0 \implies A = -B.
  • Constant term: A−B=2.A - B = 2. Substituting A=−BA = -B, we get −B−B=2⇒−2B=2⇒B=−1,-B - B = 2 \Rightarrow -2B = 2 \Rightarrow B = -1, hence A=1.A = 1.

Thus,

2(2r−1)(2r+1)=12r−1−12r+1.\frac{2}{(2r-1)(2r+1)} = \frac{1}{2r-1} - \frac{1}{2r+1}.

Step 3: Form the telescoping sum:

∑r=1n(12r−1−12r+1).\sum_{r=1}^{n}\left(\frac{1}{2r-1} - \frac{1}{2r+1}\right).

Writing out the first few terms:

(11−13)+(13−15)+⋯+(12n−1−12n+1).\left(\frac{1}{1} - \frac{1}{3}\right) + \left(\frac{1}{3} - \frac{1}{5}\right) + \cdots + \left(\frac{1}{2n-1} - \frac{1}{2n+1}\right).

Most terms cancel, leaving:

=11−12n+1=1−12n+1=2n2n+1.= \frac{1}{1} - \frac{1}{2n+1} = 1 - \frac{1}{2n+1} = \frac{2n}{2n+1}.