Question

If $\cot^{-1}\left(4+\frac{2}{4}\right)+\cot^{-1}\left(4+\frac{6}{4}\right)+\cot^{-1}\left(4+\frac{12}{4}\right)+... \infty=\tan^{-1}\left(\frac{a}{b}\right)$ where a and b are co-prime then find the value of (a+b).

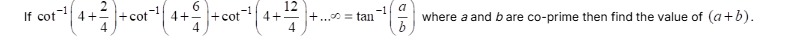
Answer 1

5

Answer 2

The general term is given by:

$T_n = \cot^{-1}\left(4+\frac{n(n+1)}{4}\right) = \tan^{-1}\left(\frac{4}{n^2+n+16}\right)$

This is a telescoping series, and the sum converges to $\tan^{-1}\left(\frac{2}{3}\right)$.

Therefore, $a = 2$ and $b = 3$, and $a+b = 5$.