Question

If $(cos^8\theta - sin^8\theta)sec2\theta = \lambda_1 - \frac{sin^2(\lambda_2\theta)}{2}$ then the maximum value of $\lambda_1 - \lambda_2$ is

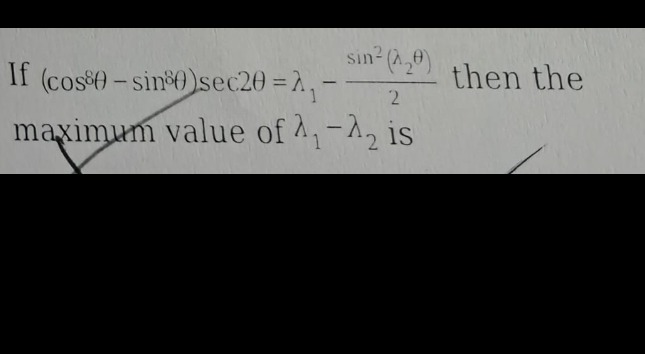
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (C)

3

Answer 2

The given equation is $(cos^8\theta - sin^8\theta)sec2\theta = \lambda_1 - \frac{sin^2(\lambda_2\theta)}{2}$. The left-hand side simplifies as: $cos^8\theta - sin^8\theta = (cos^4\theta - sin^4\theta)(cos^4\theta + sin^4\theta)$ $= (cos^2\theta - sin^2\theta)(cos^2\theta + sin^2\theta)((cos^2\theta + sin^2\theta)^2 - 2sin^2\theta cos^2\theta)$ $= cos2\theta (1 - 2(\frac{1}{2}sin2\theta)^2) = cos2\theta (1 - \frac{1}{2}sin^2(2\theta))$. So, LHS = $cos2\theta (1 - \frac{1}{2}sin^2(2\theta)) sec2\theta = 1 - \frac{1}{2}sin^2(2\theta)$. Equating this with the RHS: $1 - \frac{1}{2}sin^2(2\theta) = \lambda_1 - \frac{sin^2(\lambda_2\theta)}{2}$. For this to be an identity, $\lambda_1 = 1$ and $sin^2(2\theta) = sin^2(\lambda_2\theta)$. For $sin^2(A) = sin^2(B)$ to hold for all $\theta$, we need $A = n\pi \pm B$. So, $2\theta = n\pi \pm \lambda_2\theta$. For this to hold for all $\theta$, $n$ must be 0. Thus, $2\theta = \pm \lambda_2\theta$, which gives $\lambda_2 = 2$ or $\lambda_2 = -2$. The possible values for $\lambda_1 - \lambda_2$ are $1 - 2 = -1$ and $1 - (-2) = 3$. The maximum value is 3.