Question

If $\cos^2x \frac{dy}{dx} - y\tan2x = \cos^4x$, where $|x| < \frac{\pi}{4}$ and $y(\frac{\pi}{6}) = \frac{3\sqrt{3}}{8}$, then the constant term in the solution of the differential equation is

Answer 1

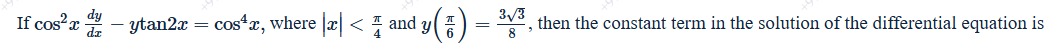
0

Answer 2

The given differential equation is $\cos^2x \frac{dy}{dx} - y\tan2x = \cos^4x$.

We can rewrite this as a first-order linear differential equation in the standard form $\frac{dy}{dx} + P(x)y = Q(x)$.

Divide the equation by $\cos^2x$: $\frac{dy}{dx} - \frac{\tan2x}{\cos^2x} y = \frac{\cos^4x}{\cos^2x}$

$\frac{dy}{dx} - (\tan2x \sec^2x) y = \cos^2x$

Here, $P(x) = -\tan2x \sec^2x$ and $Q(x) = \cos^2x$.

The integrating factor (IF) is $e^{\int P(x) dx}$.

$\int P(x) dx = \int -\tan2x \sec^2x dx$.

Let $u = \tan x$. Then $du = \sec^2x dx$.

$\tan2x = \frac{2\tan x}{1-\tan^2x} = \frac{2u}{1-u^2}$.

The integral becomes $\int -\frac{2u}{1-u^2} du$.

Let $v = 1-u^2$. Then $dv = -2u du$.

The integral is $\int \frac{dv}{v} = \ln|v| + C' = \ln|1-u^2| + C' = \ln|1-\tan^2x| + C'$.

Since $|x| < \frac{\pi}{4}$, we have $-1 < \tan x < 1$, so $0 \le \tan^2x < 1$. Thus, $1-\tan^2x > 0$.

So, $\int P(x) dx = \ln(1-\tan^2x)$.

The integrating factor is IF $= e^{\ln(1-\tan^2x)} = 1-\tan^2x$.

The general solution is given by $y \cdot IF = \int Q(x) \cdot IF dx + C$.

$y (1-\tan^2x) = \int \cos^2x (1-\tan^2x) dx + C$.

We know that $1-\tan^2x = \frac{\cos^2x - \sin^2x}{\cos^2x} = \frac{\cos2x}{\cos^2x}$.

So, $y \frac{\cos2x}{\cos^2x} = \int \cos^2x \left(\frac{\cos2x}{\cos^2x}\right) dx + C$.

$y \frac{\cos2x}{\cos^2x} = \int \cos2x dx + C$.

$y \frac{\cos2x}{\cos^2x} = \frac{1}{2}\sin2x + C$.

The solution for $y(x)$ is $y(x) = \frac{\cos^2x}{\cos2x} \left(\frac{1}{2}\sin2x + C\right)$.

This can be written as $y(x) = \frac{\cos^2x \sin2x}{2\cos2x} + C \frac{\cos^2x}{\cos2x}$.

The term $C \frac{\cos^2x}{\cos2x}$ contains the constant $C$. The question asks for "the constant term in the solution". This usually refers to the value of the constant $C$ itself, which is determined by the initial condition.

We are given the initial condition $y(\frac{\pi}{6}) = \frac{3\sqrt{3}}{8}$.

Substitute $x = \frac{\pi}{6}$ into the general solution:

$y(\frac{\pi}{6}) = \frac{\cos^2(\frac{\pi}{6})}{\cos(2 \cdot \frac{\pi}{6})} \left(\frac{1}{2}\sin(2 \cdot \frac{\pi}{6}) + C\right)$.

$\cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2}$, so $\cos^2(\frac{\pi}{6}) = (\frac{\sqrt{3}}{2})^2 = \frac{3}{4}$.

$\cos(\frac{\pi}{3}) = \frac{1}{2}$.

$\sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$.

Substitute these values and the given $y(\frac{\pi}{6})$ value:

$\frac{3\sqrt{3}}{8} = \frac{\frac{3}{4}}{\frac{1}{2}} \left(\frac{1}{2} \cdot \frac{\sqrt{3}}{2} + C\right)$.

$\frac{3\sqrt{3}}{8} = \frac{3}{2} \left(\frac{\sqrt{3}}{4} + C\right)$.

To solve for $C$, divide both sides by $\frac{3}{2}$:

$\frac{3\sqrt{3}}{8} \cdot \frac{2}{3} = \frac{\sqrt{3}}{4} + C$.

$\frac{\sqrt{3}}{4} = \frac{\sqrt{3}}{4} + C$.

This implies $C = 0$.

The constant term in the solution, which is the value of $C$, is 0.