Solveeit Logo
Login

Question

Question: If \( \cos \theta =\dfrac{2}{3} \) , then \( 2{{\sec }^{2}}\theta +2{{\tan }^{2}}\theta -7 \) is equ...

If cos⁡θ=23\cos \theta =\dfrac{2}{3} , then 2sec⁡2θ+2tan⁡2θ−72{{\sec }^{2}}\theta +2{{\tan }^{2}}\theta -7 is equal to:
A. 1
B. 0
C. 3
D. 4

Explanation

Solution

First of all apply the trigonometric identity 1+tan⁡2θ=sec⁡2θ1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta in the given expression. Convert the given expression in terms of sec⁡2θ{{\sec }^{2}}\theta . Now, it is given that cos⁡θ=23\cos \theta =\dfrac{2}{3} and we know that the reciprocal of cos⁡θ\cos \theta is sec⁡θ\sec \theta and then substitute the value of sec⁡θ\sec \theta in the given expression and solve.

Complete step-by-step answer:
The expression given in the question is:
2sec⁡2θ+2tan⁡2θ−72{{\sec }^{2}}\theta +2{{\tan }^{2}}\theta -7
Now, we are going to convert the above expression in terms of sec⁡θ\sec \theta using the trigonometric identity:
1+tan⁡2θ=sec⁡2θ ⇒tan⁡2θ=sec⁡2θ−1 \begin{aligned} & 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \\\ & \Rightarrow {{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1 \\\ \end{aligned}
Substituting the above value of tan⁡2θ{{\tan }^{2}}\theta in the given expression we get,
2(sec⁡2θ+tan⁡2θ)−7 =2(sec⁡2θ+sec⁡2θ−1)−7 =4sec⁡2θ−9 \begin{aligned} & 2\left( {{\sec }^{2}}\theta +{{\tan }^{2}}\theta \right)-7 \\\ & =2\left( {{\sec }^{2}}\theta +{{\sec }^{2}}\theta -1 \right)-7 \\\ & =4{{\sec }^{2}}\theta -9 \\\ \end{aligned}
It is given that:
cos⁡θ=23\cos \theta =\dfrac{2}{3}
As we have converted the given expression in terms of sec⁡θ\sec \theta so we need the value of sec⁡θ\sec \theta . We have given the value of cos⁡θ\cos \theta so from the trigonometry we know that the inverse of cos⁡θ\cos \theta is sec⁡θ\sec \theta . So, taking the reciprocal of cos⁡θ\cos \theta we get,
sec⁡θ=32\sec \theta =\dfrac{3}{2}
Substituting this value of sec⁡θ\sec \theta in the expression 4sec⁡2θ−94{{\sec }^{2}}\theta -9 we get,
4(32)2−9 =4(94)−9 =9−9=0 \begin{aligned} & 4{{\left( \dfrac{3}{2} \right)}^{2}}-9 \\\ & =4\left( \dfrac{9}{4} \right)-9 \\\ & =9-9=0 \\\ \end{aligned}
From the above calculation, the value of the given expression is 0.
Hence, the correct option is (b).

Note: In the above solution instead of using the identity 1+tan⁡2θ=sec⁡2θ1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta we can substitute the value of the tan θ in the given expression 2sec2θ + 2tan2θ – 7. Now, we can find the value of tan θ as follows:
cos⁡θ=23\cos \theta =\dfrac{2}{3}
In the below diagram, we have shown a triangle ABC right angled at B along with an angle θ\theta .

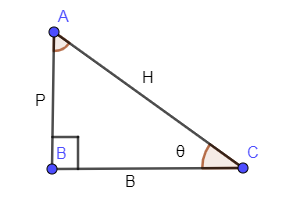
In the above figure, “P” stands for perpendicular with respect to angle θ, “B” stands for the base with respect to angle θ and “H” stands for the hypotenuse with respect to angle θ.

We know that, cos⁡θ\cos \theta is equal to base divided by hypotenuse so using Pythagoras theorem we can find the perpendicular of the triangle.
cos⁡θ=BH\cos \theta =\dfrac{B}{H}
H2=B2+P2 ⇒9=4+P2 ⇒P2=5 ⇒P=5 \begin{aligned} & {{H}^{2}}={{B}^{2}}+{{P}^{2}} \\\ & \Rightarrow 9=4+{{P}^{2}} \\\ & \Rightarrow {{P}^{2}}=5 \\\ & \Rightarrow P=\sqrt{5} \\\ \end{aligned}
From the above calculation, we can find the value of tan⁡θ\tan \theta :
tan⁡θ=52\tan \theta =\dfrac{\sqrt{5}}{2}
Substituting this value of tan⁡θ\tan \theta in the given expression we get,

& 2\left( {{\sec }^{2}}\theta +{{\tan }^{2}}\theta \right)-7 \\\ & =2\left( \dfrac{9}{4}+\dfrac{5}{4} \right)-7 \\\ & =2\left( \dfrac{14}{4} \right)-7 \\\ & =7-7=0 \\\ \end{aligned}$$ Hence, we have got the answer as 0.