Solveeit Logo
Login

Question

Question: If \(\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right)\) is equa...

If cos⁡(540∘−θ)−sin⁡(630∘−θ)\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) is equal to
A.0
B.2cos⁡θ2\cos \theta
C.2sin⁡θ2\sin \theta
D.sin⁡θ−cos⁡θ\sin \theta - \cos \theta

Explanation

Solution

Here, we will break the given angle into two angles such that we know the value of either of the angles or that angle is present on the quadrants. After breaking the angle, we will solve them using quadrants for trigonometric function and hence, find the required answer.

Complete step-by-step answer:
We have to solve cos⁡(540∘−θ)−sin⁡(630∘−θ)\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right).
First of all, we will draw the quadrants:

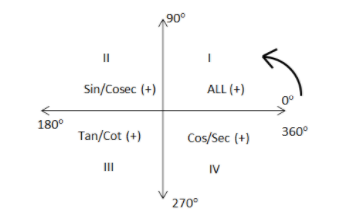
Now, 540∘540^\circ can be written as:
540∘=(360∘+180∘)540^\circ = \left( {360^\circ + 180^\circ } \right)
Also, 630∘630^\circ can be written as:
630∘=(360∘+270∘)630^\circ = \left( {360^\circ + 270^\circ } \right)
Hence, substituting these values in the given expression, we get
⇒cos⁡(540∘−θ)−sin⁡(630∘−θ)=cos⁡(360∘+180∘−θ)−sin⁡(360∘+270∘−θ)\Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = \cos \left( {360^\circ + 180^\circ - \theta } \right) - \sin \left( {360^\circ + 270^\circ - \theta } \right)
Now, cos⁡360∘\cos 360^\circ means one complete rotation.
Since, cos⁡360∘\cos 360^\circ lies nearly on the fourth quadrant and on the fourth quadrant cos⁡θ\cos \theta is positive.
Therefore, cos⁡360∘\cos 360^\circ is also positive.
Now, when we add any angle to cos⁡360∘\cos 360^\circ it means that we are starting the second rotation. Hence, we usually neglect 360∘360^\circ while solving trigonometric questions.
Now, cos⁡(360∘+180∘−θ)−sin⁡(360∘+270∘−θ)\cos \left( {360^\circ + 180^\circ - \theta } \right) - \sin \left( {360^\circ + 270^\circ - \theta } \right) can be written as:
⇒cos⁡(540∘−θ)−sin⁡(630∘−θ)=cos⁡(180∘−θ)−sin⁡(270∘−θ)\Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = \cos \left( {180^\circ - \theta } \right) - \sin \left( {270^\circ - \theta } \right)
Now, when we subtract any angle from 180∘180^\circ , then, we reach the second quadrant.
In the second quadrant, cosine is negative and due to 180∘180^\circ , the trigonometric function will remain the same.
Also, when we subtract any angle from 270∘270^\circ , then, we reach the third quadrant.
In the third quadrant, sine is negative and also, due to 270∘270^\circ , the trigonometric function will change, i.e. sine will change to cosine.
⇒cos⁡(540∘−θ)−sin⁡(630∘−θ)=−cos⁡θ−(−cos⁡θ)\Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = - \cos \theta - \left( { - \cos \theta } \right)
⇒cos⁡(540∘−θ)−sin⁡(630∘−θ)=−cos⁡θ+cos⁡θ=0\Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = - \cos \theta + \cos \theta = 0
Therefore, cos⁡(540∘−θ)−sin⁡(630∘−θ)\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) is equal to 0.
Hence, option A is the correct answer.

Note: We should take care while solving the quadrants because in one quadrant cosine/sine is positive and in the other it is negative. If we use 0∘,180∘0^\circ ,180^\circ or 360∘360^\circ then the trigonometric functions remain the same. But if we use 90∘90^\circ or 270∘270^\circ , then we have changed the trigonometric function. Also, we can break the given angle in any sum possible but we should keep in mind that we have to break it in such a sum such that we know the value of one of those or how to solve the question using one of those angles.