Question

If complex numbers $\overline{z_1},\overline{z_2},\overline{z_3},\overline{z_4}$ are the roots of the equation $z^4 = 1$ then the value of $|z_1^4 + z_2^4 + z_3^4 + z_4^4|$ is equal to ____.

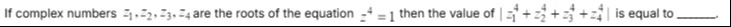
Answer 1

4

Answer 2

Let $\overline{z_1}, \overline{z_2}, \overline{z_3}, \overline{z_4}$ be the roots of $z^4 = 1$. The 4th roots of unity are $1, i, -1, -i$.

Since the conjugate of a root is still a 4th root of unity (because the conjugate of $z^4$ equals $(\overline{z})^4$), we have:

$$z_1^4 = z_2^4 = z_3^4 = z_4^4 = 1.$$

Thus,

$$z_1^4 + z_2^4 + z_3^4 + z_4^4 = 1 + 1 + 1 + 1 = 4.$$

Taking the absolute value:

$$\left| z_1^4 + z_2^4 + z_3^4 + z_4^4 \right| = |4| = 4.$$

Core Explanation

Each term $z_i^4$ equals 1, so the sum is 4 and its absolute value is 4.