Question

If circles $x^2 + y^2 + 2x + 4y + 1 = 0$ and $x^2 + y^2 + 2gx + 2fy + 3 = 0$ are orthogonal, then $(8g + 16f)$ is

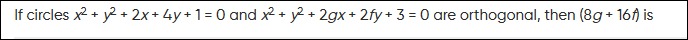
Answer 1

16

Answer 2

The condition for orthogonality of two circles $x^2 + y^2 + 2u_1x + 2v_1y + c_1 = 0$ and $x^2 + y^2 + 2u_2x + 2v_2y + c_2 = 0$ is $2u_1u_2 + 2v_1v_2 = c_1 + c_2$. For the given circles, $u_1=1, v_1=2, c_1=1$ and $u_2=g, v_2=f, c_2=3$. Applying the condition yields $2(1)(g) + 2(2)(f) = 1+3$, simplifying to $2g+4f=4$. The expression to evaluate is $8g+16f$, which is $4(2g+4f)$. Substituting the derived relation, $8g+16f = 4(4) = 16$.