Question

If circles are drawn taking two sides of a triangle as a diameter, prove that the point of intersection of these circles lies on the third side.

Answer 1

Here, in this question we will use the theorem of semicircle which says that the angle made by the diameter in semicircle is always the right angle.

Complete step-by-step solution
Given,
In $\Delta ABC$ side AB as a diameter of circle ${C_1}$ and side AC as a diameter of circle ${C_2}$.
The following is the diagram of the two circles ${C_1}$ and ${C_2}$ in which AB and AC are the sides of a triangle ABC.

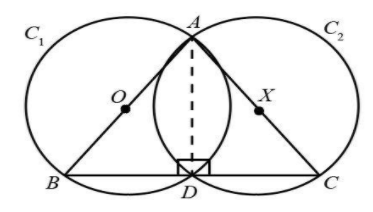
Construction
Join AD.
In$\Delta ABD$, angle made by the diameter in the semicircle is $\angle ADB$ will be equal to right angle.
$\angle ADB = 90^\circ$…..(1)
In$\Delta ACD$, angle made by the diameter in the semicircle is $\angle ADC$ will be equal to right angle.
$\angle ADC = 90^\circ$…...(2)
Add equation (1) and (2) we get
$\begin{array}{c} \angle ADB + \angle ADB = 90^\circ + 90^\circ \\\ = 180^\circ \end{array}$

It means $\angle ADB$ and $\angle ADC$ are linear pair angles and we know that linear pair angle is always formed on a straight line. The circle described on line AC as diameter will pass through point D because of which the two circles ${C_1}$ and ${C_2}$ intersects at point D.
Thus, the point of intersection D of circle ${C_1}$ and ${C_2}$ lies on line BC which is the third side of the triangle.

Note: The tricky part in this question is that if we prove that the intersection point of circles lies on a straight line then this straight line will automatically become the third side of the triangle and hence we can prove that the point of intersection of these circles lies on the third side.