Question

If circle with center $\left( {0,0} \right)$ touches the line $5x + 12y = 1$ then it equation will be
(A) $169\left( {{x^2} + {y^2}} \right) = 1$
(B) $\left( {{x^2} + {y^2}} \right) = 169$
(C) $16\left( {{x^2} + {y^2}} \right) = 1$
(D) $\left( {{x^2} + {y^2}} \right) = 13$

Answer 1

Hint : Equation of a circle with center at origin and radius $r$ can be written as
${x^2} + {y^2} = {r^2}$ this is also known as the standard form of the circle where x and y are points on the coordinate axes.

Complete step-by-step answer :
As we know, equation of a circle with center at origin $(0,0)$ and radius $r$ can be written as
${x^2} + {y^2} = {r^2}$
The line $5x + 12y = 1$ touches the circle. That means, it is a tangent to the given circle.
Observe the diagram

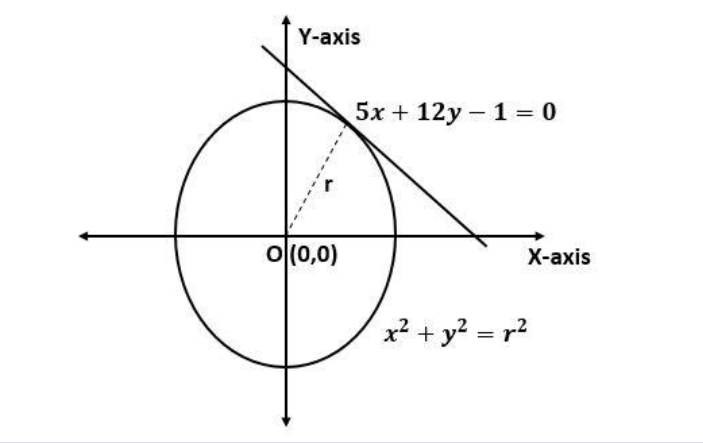
From the diagram, we can conclude that the distance between the tangent and the center of the circle will be equal to the radius of the circle.
Distance of a point $({x_1},{y_1})$ from a line $ax + by + c = 0$ is given by
$d = \left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$ . . . (1)
Rewrite the equation of line $5x + 12y = 1$ in standard form as $5x + 12y - 1 = 0$
Then using equation (1), we can write
$r = \left| {\dfrac{{5 \times 0 + 12 \times 0 - 1}}{{\sqrt {\left( {{5^2}} \right) + {{\left( {12} \right)}^2}} }}} \right|$
$= \left| {\dfrac{{ - 1}}{{\sqrt {169} }}} \right|$
$= \left| {\dfrac{{ - 1}}{{13}}} \right|$
$\Rightarrow r = \dfrac{1}{{13}}$
So, equation of circle can be written as
${x^2} + {y^2} = {\left( {\dfrac{1}{{13}}} \right)^2}$
$\Rightarrow {x^2} + {y^2} = \dfrac{1}{{169}}$
By cross multiplying, we get
$169({x^2} + {y^2}) = 1$
Therefore, from the above explanation, the correct answer is, option (A) $169({x^2} + {y^2}) = 1$
So, the correct answer is “Option A”.

Note : To solve this question you need to know the equation of the circle passing through origin. And you also need to know that a tangent always touches a circle at only one point on its circumference, hence, the distance from the center of the circle to the tangent is always equal to the radius of the circle. Unless and until it is specified, the distance of a point to any line is always taken as the shortest distance or perpendicular distance.