Question
Question: If circle \(S\left( x,y \right)=0\) touches the line \(x+y-5=0\) at \(\left( 2,3 \right)\) and \(S\l...
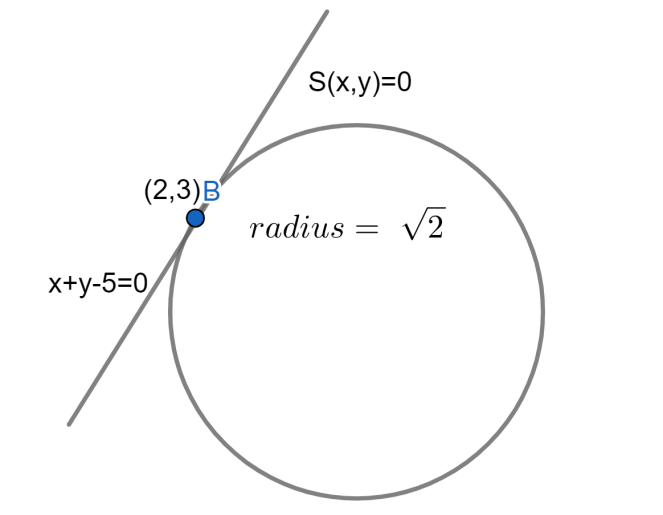
If circle S(x,y)=0 touches the line x+y−5=0 at (2,3) and S(1,2)=−2 the radius of the circle is
Solution
From the question given we have to find the radius of the circle of S(x,y)=0. To find the radius of circle, firstly we know the general equation for the intersection of line and circle is (x−h)2+(y−k)2+λ(line equation)=0 where λ is any constant after finding the value of λ. We will get a circle equation and then for the general circle equation x2+y2+2gx+2fy+c=0 to find the radius the formula is radius=(g2+f2−c)
Complete step-by-step solution:
From the given question the circle S(x,y)=0 touches the line x+y−5=0 at (2,3)
Now, after comparing with the general equation of intersection of line and circle. The circle equation can be written.
And from the question we also know that the S(1,2)=−2.
We also know that (2,3), is a point on the circle
By this we can say that,
⇒(h,k)=(2,3)
As we know that the general equation of circle for the intersection of line and circle is
⇒(x−h)2+(y−k)2+λ(line equation)=0
In the question itself we know the equation of line that is
⇒line equation=x+y−5=0
Now by substituting in their respective positions in the circle equation we will get,
⇒(x−2)2+(y−3)2+λ(x+y−5)=0
As we already know that S(1,2)=−2.
So, by using this we will get value of λ
By substituting the values, we will get,
⇒(1−2)2+(2−3)2+λ(1+2−5)=−2
⇒(−1)2+(−1)2+λ(−2)=−2
⇒−2λ=−4
⇒λ=2
Therefore, we got the value of λis 2
With this we got the circle equation that is
⇒(x−2)2+(y−3)2+2(x+y−5)=0
By simplifying further
⇒x2+4−4x+y2−6y+9+2x+2y−10=0
⇒x2+y2−2x−4y+3=0
Therefore, the circle equation is x2+y2−2x−4y+3=0
As we know that the radius of the general equation of a circle is
⇒x2+y2+2gx+2fy+c=0
For the above equation the radius is
⇒radius=(g2+f2−c)
By this the radius of the S(x,y)=0 is
By comparing the results are
⇒g=−1
⇒f=−2
⇒c=3
By substituting these values in the above formula, we will get radius
⇒radius=(g2+f2−c)
⇒r=(−1)2+(−2)2−3
⇒r=1+4−3
⇒r=2
Therefore, the radius of the circle is r=2
The figure for the question will be as follows.
Note: Students should know the concept of circle like, the general circle equation x2+y2+2gx+2fy+c=0 and its radius and centre is centre=(−g,−f), radius=(g2+f2−c). The general equation of a circle whose centre is origin is x2+y2=r2 where r is the radius of the circle.
