Question

If C is the midpoint of the line segment joining A (4,0) and B (0,6) and if O is the origin, then show that C is equidistant from all the vertices from $\Delta OAB$.

Answer 1

In order to solve this problem, we need to find the value of the coordinates of point C. We can find the coordinates of the midpoint of any segment by using the midpoint formula. It is given as follows, $\text{Midpoint}=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ , where ${{x}_{1}},{{x}_{2}}$ are x coordinates and ${{y}_{1}},{{y}_{2}}$ are the y coordinates. Also, we need to know the distance formula which is given as follows, $\text{Distance}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .

Complete step-by-step solution:
To understand the question better we need to draw the diagram.

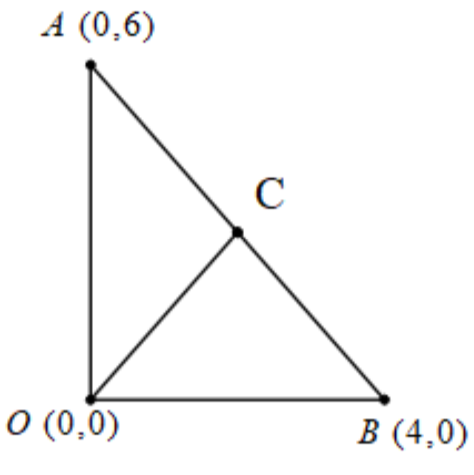
We are given that C is the midpoint of the segment AB. And we need to show that C is equidistant from all the vertices of $\Delta OAB$.
The vertices of the $\Delta OAB$ are points O, A, and B.
Then we need to show that OA = OB = OC
For finding the distance we need to find the coordinates of C.
We know that C is the midpoint of segment AB.
The formula for the midpoint is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ .
Where ${{x}_{1}},{{x}_{2}}$ are x coordinate and ${{y}_{1}},{{y}_{2}}$ are the y coordinates.
Substituting the values we get,
Point C = $\left( \dfrac{0+4}{2},\dfrac{6+0}{2} \right)=\left( 2,3 \right)$
Now we have the coordinates of all the four points.
The formula for distance between two points is given as follows,
$\text{Distance}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ , where ${{x}_{1}},{{x}_{2}}$ are x coordinate and ${{y}_{1}},{{y}_{2}}$ are the y coordinates.
Now let's first calculate the distance of segment CA.
Substituting the values of x coordinates and y coordinates we get,
$CA=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 3-6 \right)}^{2}}}$
Solving this equation, we get,
$\begin{aligned} & CA=\sqrt{4+{{\left( -3 \right)}^{2}}} \\\ & =\sqrt{4+9} \\\ & =\sqrt{13} \end{aligned}$
Now let’s find the distance of segment CB.
Substituting the values of x coordinates and y coordinates we get,
$CB=\sqrt{{{\left( 2-4 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}$
Solving this equation, we get,
$\begin{aligned} & CA=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 3 \right)}^{2}}} \\\ & =\sqrt{4+9} \\\ & =\sqrt{13} \end{aligned}$
Now let’s find the distance of segment CO.
Substituting the values of x coordinates and y coordinates we get,
$CO=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}$
Solving this equation, we get,
$\begin{aligned} & CO=\sqrt{4+9} \\\ & =\sqrt{13} \end{aligned}$
We can see that the distance between CA = CB = CO.

Hence, we can say that C is equidistant from all the vertices of $\Delta OAB$.

Note: In this problem, we need to use the distance formula. We can assign any value as ${{x}_{1}}$ and ${{x}_{2}}$ as we are going to square that number anyways. But we need to be careful that whenever we assign an x coordinate as ${{x}_{1}}$ we need to assign the same point as ${{y}_{1}}$. A similar process can be applied for finding the midpoint.