Question

If C is the midpoint of $AB$ and $P$ is any point outside $AB$, then \overrightarrow{PA}+\overrightarrow{PB}=\\_\\_\\_\\_\\_.

Answer 1

We recall the definition of vector, head and tail of the vector, the addition of vectors using triangle law. We use triangle law of addition of vectors in vector triangles PAC and PBC to express $\overrightarrow{PA},\overrightarrow{PB}$ as resultant of $\overrightarrow{PC},\overrightarrow{CA}$ and $\overrightarrow{PC},\overrightarrow{CB}$ respectively.

Complete step-by-step solution
We know that a vector is a geometric object that has magnitude and direction. It is represented by an arrow where the tip of the arrow represents the direction and the length of the arrow represents the magnitude. The tip of the arrow is called the head of the vector and the other end of the arrow is the tail of the vector. We represent $\overrightarrow{a}$ with tail A and head B can be represented as $\overrightarrow{AB}$.$$$$

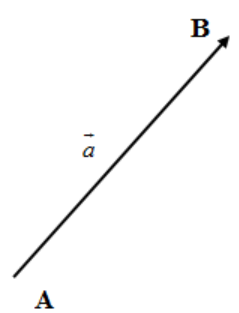
We know from vector algebra how to add two vectors by head to tail method. If the head of $\overrightarrow{a}=\overrightarrow{AB}$ coincides with the tail of $\overrightarrow{b}=\overrightarrow{BC}$ ;then resultant vector is represented by say $\overrightarrow{r}=\overrightarrow{AC}$. This method is also called a triangle because $A,B,C$ form a triangle. We have

& \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} \\\ & \Rightarrow \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{r} \\\ \end{aligned}$$  We are given in the question $C$ is the midpoint of $AB$ and $P$ is any point outside$AB$. We are asked to find the resultant vector of $\overrightarrow{PA},\overrightarrow{PB}$. Let us draw its vector diagram including $\overrightarrow{CA},\overrightarrow{CB}, \overrightarrow{PC}$.  Since $C$ is the midpoint of AB, the vectors $\overrightarrow{CA},\overrightarrow{CB}$ will be magnitudes and according to our construction will be in the opposite direction. So we have, $$\begin{aligned} & \overrightarrow{CA}=-\overrightarrow{CB} \\\ & \Rightarrow \overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{0}.......\left( 1 \right) \\\ \end{aligned}$$ We use the triangle law in triangle PAC to represent $\overrightarrow{PA}$ as the resultant of $\overrightarrow{PC}$ and $\overrightarrow{CA}$ since head of $\overrightarrow{PC}$ is the tail of $\overrightarrow{CA}$. So we have $$\overrightarrow{PA}=\overrightarrow{PC}+\overrightarrow{CA}......\left( 2 \right)$$ We use the triangle law in triangle PBC to represent $\overrightarrow{PB}$ as the resultant of $\overrightarrow{PC}$ and $\overrightarrow{CB}$ since head of $\overrightarrow{PC}$ is the tail of $\overrightarrow{CB}$. So we have $$\overrightarrow{PB}=\overrightarrow{PC}+\overrightarrow{CB}.....\left( 3 \right)$$ Let us add corresponding sides of equation (2) and (3) to have; $$\begin{aligned} & \Rightarrow \overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PC}+\overrightarrow{CA}+\overrightarrow{CB} \\\ & \Rightarrow \overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PC}\left( \because \overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{0} \right) \\\ \end{aligned}$$ So we need to fill $2\overrightarrow{PC}$ in the blank. **Note:** We can also add vectors using the parallelogram law where the diagonal represents the resultant vector. We note that vector addition is commutative and associative. We need to be careful that $\overrightarrow{CA}+\overrightarrow{CB}$ is a vector called zero or null vector $\left( \overrightarrow{0} \right)$ with arbitrary direction not the number zero (0).