Question

If $C,D$ are two events such that $C \subset D$ and $P(D) \ne 0$, then correct statement among the following is:
A. $P\left( {\dfrac{C}{D}} \right) = P(C)$
B. $P\left( {\dfrac{C}{D}} \right) \geqslant P(C)$
C. $P\left( {\dfrac{C}{D}} \right) < P(C)$
D. $P\left( {\dfrac{C}{D}} \right) = \dfrac{{P(D)}}{{P(C)}}$

Answer 1

We are given that $C,D$ are two events such that $C \subset D$ and$P(D) \ne 0$.In order to solve the question, we can clearly see from options that conditional probability is included.So, we consider the conditional probability $P\left( {\dfrac{C}{D}} \right)$ and then use $C \subset D$, which is given.

Complete step-by-step answer:
In this question, we are given that $C,D$ are two events such that $C \subset D$ and $P(D) \ne 0$.
Now from the question, we know that we need to find a conditional probability.
We know that if $A$ and $B$, are any two events then probability of $A$, when $B$ has already occurred is conditional probability-
$P\left( {\dfrac{{\text{A}}}{{\text{B}}}} \right) = \dfrac{{P({\text{A}} \cap {\text{B}})}}{{P({\text{B}})}}$.
Hence from above we can see that to find conditional probability we need to find the probability of intersection of that event.
So, to find conditional probability $P\left( {\dfrac{C}{D}} \right)$, we firstly find the probability of intersection of $C,D$.
Now to find the probability of intersection of $C,D$ we will use $C \subset D$
Now firstly consider that,
$C \subset D$ and therefore, we can write that using the given Venn diagram-

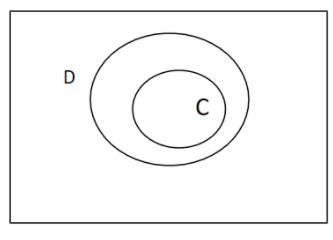
$C \cap D = C$
Now taking probability on both the sides we get
$P(C \cap D) = P(C)$ $- - - - - (1)$
Now we consider the conditional probability $P\left( {\dfrac{C}{D}} \right)$
We also know using the definition of conditional probability
We know that if $A$ and $B$, are any two events then probability of $A$, when $B$ has already occurred is conditional probability-
$P\left( {\dfrac{{\text{A}}}{{\text{B}}}} \right) = \dfrac{{P({\text{A}} \cap {\text{B}})}}{{P({\text{B}})}}$.$- - - - (2)$
Now substituting events $C,D$ in (2), we get
$P\left( {\dfrac{C}{D}} \right)$ $= \dfrac{{P(C \cap D)}}{{P(D)}}$ $- - - - (3)$
Now substituting the value of $P(C \cap D)$ from (1) in (3), we get,
$P\left( {\dfrac{C}{D}} \right)$ $= \dfrac{{P(C)}}{{P(D)}}$ $- - - - - (3)$
Now we also know that for any event ${\text{A}}$, then
$0 \leqslant P(A) \leqslant 1$
Now we are given that $D{\text{ is a event}}$ and therefore we can say that
$0 < P(D) \leqslant 1,P(D) \ne 0$
We can also write that-
$\Rightarrow P(D) \leqslant 1$
Taking reciprocal on both the sides, we get
$\dfrac{1}{{P(D)}} \geqslant 1$, it is defined because we are given that $P(D) \ne 0$
Now multiplying $P(C)$ on both the sides, we get,
$\left( {\dfrac{{P(C)}}{{P(D)}}} \right)$ $\geqslant P(C)$
Now substituting value of $\left( {\dfrac{{P(C)}}{{P(D)}}} \right)$ in (3), we get,
$P\left( {\dfrac{C}{D}} \right)$ $\geqslant P(C)$

So, the correct answer is “Option B”.

Note: In this question, we are given that $C \subset D$ and we can write it as $C \cap D = C$ by using the venn diagram.Also, we can say that if $C \subset D$, then we get that $P(C) \subset P(D)$.Now we can also write that $P(C \cap D) = P(C)$.So, in this way we can solve this question.Generally, students are not able to think about using this inequality $0 \leqslant P(A) \leqslant 1$ , So we should always remember that if in questions of probability, any inequality is involved, then we must use this $0 \leqslant P(A) \leqslant 1$.