Question
Question: If \(C = 50\mu F\)in the figure below, What is the equivalent capacitance between points A and B? ...
If C=50μFin the figure below,
What is the equivalent capacitance between points A and B?
Repeat for points A and D.
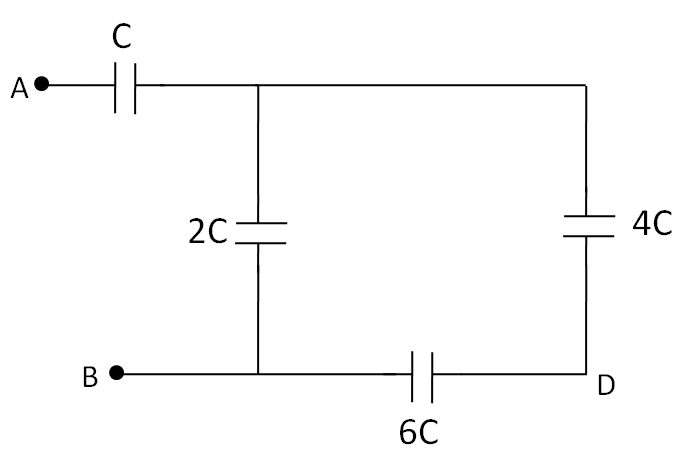
Solution
Hint
To solve this question, we need to imagine a battery across the points where the equivalent capacitance is required. Then, identifying the series and parallel combinations, apply the suitable formulae for the equivalent capacitance.
The formulae used in this solution are
⇒Cs1=C11+C21+...........
⇒Cp=C1+C2+...........
Where Cs is the equivalent series capacitance, and Cp is the equivalent parallel capacitance of the capacitances C1,C2……..
Complete step by step answer
(A) We first imagine that a battery is connected between the point A and B, as shown in the figure below.
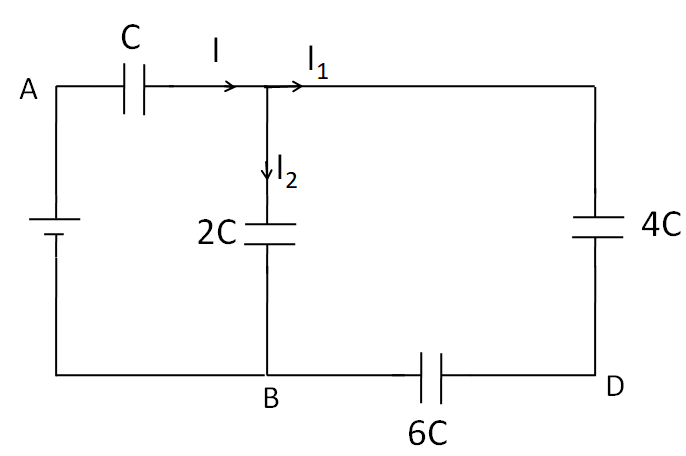
According to the current distribution in the figure, we can see that the same current I1 is flowing through 4C and 6C capacitances. So these two capacitances are in series.
So the equivalent capacitance of 4C and 6C capacitances is given as
⇒Cs1=4C1+6C1
Taking the LCM, we get
⇒Cs1=12C3+2
Taking reciprocal, we have
⇒Cs=512C
Now, the above circuit is reduced to
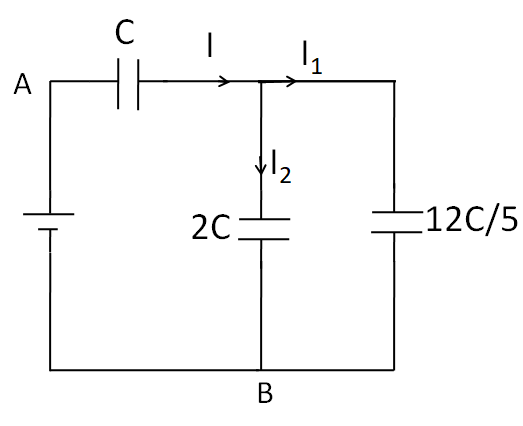
As the capacitances 2C and 512C are end to end connected, so they form a parallel combination. The equivalent capacitance of 2Cand 512C capacitances is given by
⇒Cp=2C+512C
⇒Cp=522C
Now, the above circuit reduces to
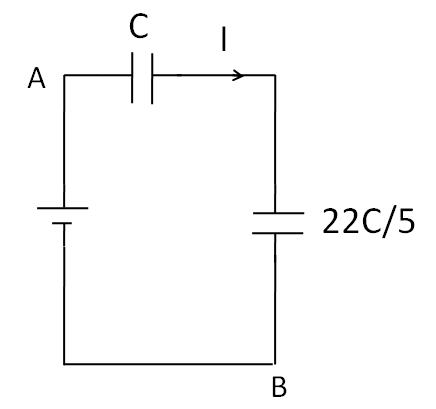
As the same current Iis flowing through Cand 522Ccapacitances. So these two capacitances are in series. So the equivalent capacitance of Cand ⇒522Ccapacitances is given as
⇒Cs1=C1+522C1
⇒Cs1=C1+22C5
Taking the LCM, we get
⇒Cs1=22C27
Taking reciprocal
⇒Cs=2722C
As only this capacitance is left, this is the equivalent capacitance between the points A and B. Substituting C=50μF
⇒Cs=2722×50=40.74μF
(B) Now, we imagine a battery between points B and D, as shown in the figure below.
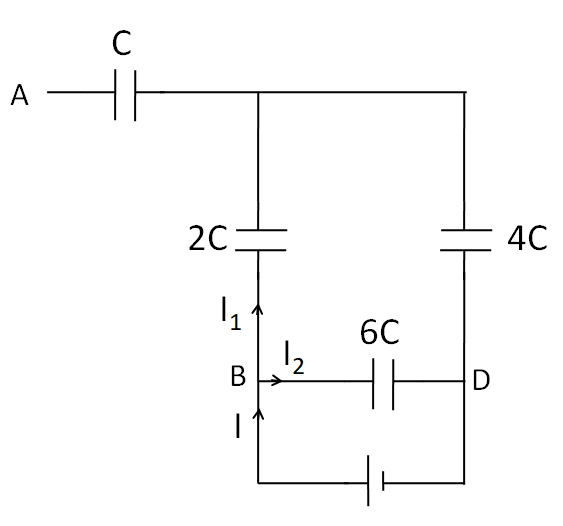
As the left end of the capacitance Cis not connected to any point, no current will flow through it, so it can be taken out of the circuit. Thus, the circuit reduces to
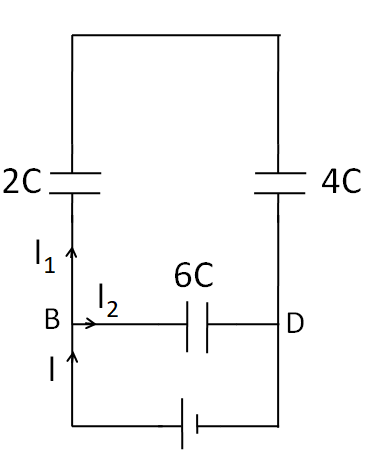
As the same current I1 is flowing through 4C and 2C capacitances. So these two capacitances are in series.
So the equivalent capacitance of 4C and 2C capacitances is given as
⇒Cs1=4C1+2C1
Taking the LCM, we get
⇒Cs1=4C3
Taking reciprocal, we have
⇒Cs=34C
Now, the above circuit is reduced to
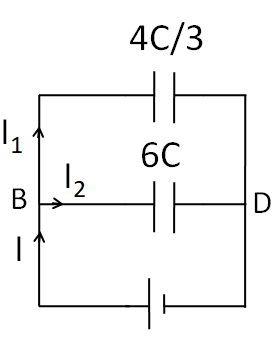
As the capacitances 6C and 34C are end to end connected, so they form a parallel combination. The equivalent capacitance of 6C and 34C capacitances is given by
⇒Cp=6C+34C
⇒Cp=322C
As only this capacitance is left, so this is the equivalent capacitance between the points B and D.
Substituting C=50μF
⇒Cs=322×50=366.67μF
Hence, the equivalent capacitance between the points A and B is 40.74μF and between the points B and D is 366.67μF.
Note
The current distributions shown in the diagrams after connecting a virtual battery are just for identifying the combinations of capacitances. They do not have any theoretical significance. As we all know, that under a DC source, a capacitor behaves as an open circuit, so the current in the circuit would be zero. The current distributions although not being theoretically correct, help us in identifying the series and parallel combinations of capacitances, just like we do in the case of resistances.
