Question

If c = 3a-2b then the value of a (b x c) =

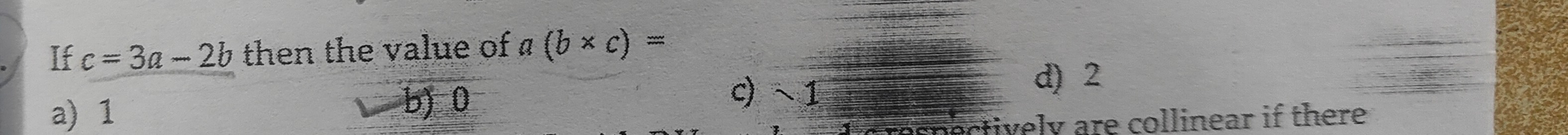
• A. 1
• B. 0
• C. ~1
• D. 2

Answer 1

Answer: (B)

0

Answer 2

Given

$$\mathbf{c} = 3\mathbf{a} - 2\mathbf{b}.$$

We need to evaluate:

$$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \mathbf{a} \cdot \left(\mathbf{b} \times (3\mathbf{a} - 2\mathbf{b})\right).$$

Using the distributive property of the cross product:

$$\mathbf{b} \times (3\mathbf{a} - 2\mathbf{b}) = 3 (\mathbf{b} \times \mathbf{a}) - 2 (\mathbf{b} \times \mathbf{b}).$$

Since $\mathbf{b} \times \mathbf{b} = \mathbf{0}$, we have:

$$\mathbf{b} \times (3\mathbf{a} - 2\mathbf{b}) = 3 (\mathbf{b} \times \mathbf{a}).$$

Thus,

$$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = 3 \, \mathbf{a} \cdot (\mathbf{b} \times \mathbf{a}).$$

Note that the scalar triple product $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{a})$ is zero because $\mathbf{b} \times \mathbf{a}$ is perpendicular to $\mathbf{a}$. Hence,

$$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = 3\times 0 = 0.$$

Using the distributive property and noting that $\mathbf{b} \times \mathbf{b} = \mathbf{0}$ and $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{a}) = 0$, we get the final answer as 0.