Question
Question: If block A is moving with an acceleration of \(5m/{{s}^{2}}\) , the acceleration of B w.r.t. ground ...
If block A is moving with an acceleration of 5m/s2 , the acceleration of B w.r.t. ground is:
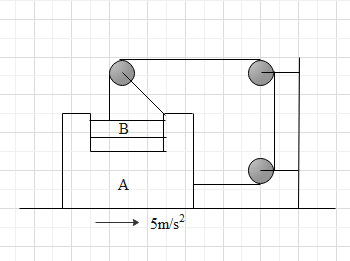
A. 5m/s2B. 52m/s2C. 55m/s2D. 10m/s2
Solution
From the diagram we can observe that the block B will have two accelerations. One is due to the acceleration of the block A in the same direction and the other is vertically downward. The vertical acceleration can be found from the change in length of the string in the different parts due to the movement of the block A. Then we can find the resultant acceleration with the help of vector addition.
Complete step by step answer:
The block A and block B are connected to each other by a string of constant length. Again, block B is always in contact with the block A. so, the block B will have two accelerations. Because block B is always in contact with the block A, block B will have a horizontal acceleration equal to the acceleration of block A. Again, when the block A accelerates towards right, block B will accelerate towards the bottom direction. So, block B will also have a vertical acceleration. We can find the total acceleration by vector addition of these two accelerations.

Given, block A is accelerating towards right with a=5ms−2
Now, the horizontal acceleration of the block B is equal to the acceleration of the block A. so,
a1=a=5ms−2
Now, the total length of the string is constant. So, we can write that,
l1+l2+l3+l4=constant
Double differentiating both sides of the above equation with respect to time, we get that,
d2td2l1+d2td2l2+d2td2l3+d2td2l4=0
Now, since the block A is accelerating, the lengths l1, l3 and l4 will change according to the acceleration. But the length l2 will not change, because the distance between the two pulleys is constant. So, we can write,
−a+0−a+a2=0a2=2a
The negative sign before a is because the length of the string is decreasing with time.
We get that, a1=a and a2=2a
Taking the vector sum of these two, we get that the acceleration of the block B is,
aB=a12+a22aB=a2+(2a)2aB=5a2aB=a5
Putting the value of a we get that the acceleration of block B is aB=55ms−2
So, the correct answer is “Option C”.
Note: When we find the acceleration from the change in lengths of the string in different parts, due to the change in length of l1 and l3 will be negative. This is because due to the acceleration of block A, with time the lengths will decrease. But, due to the change in l4 the acceleration is positive. This is because with time the length will increase because of acceleration of block A.
